题目内容

求证：sin4α+cos4α=1-2sin2αcos2α
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：已知等式左边利用完全平方公式变形，计算得到结果与右边相等，得证．
解答： 证明：左边=（sin2α+cos2α）2-2sin2αcos2α=1-2sin2αcos2α=右边，
则sin4α+cos4α=1-2sin2αcos2α．
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
∫
π
2
0
sin2
x
2
dx=
 
．
已知函数f（x）=sin
πx
3
，则f（1）+f（2）+f（3）+…+f（2010）+f（2014）=
 
．
在等比数列{an}中，a2=
1
3
，a5=
1
81

（1）求数列{an}的通项公式；
（2）令bn=log9an，求数列{bn}的前n项和Tn．
若向量
BA
=（2，3），
CA
=（4，7），则
BC
=
 
．
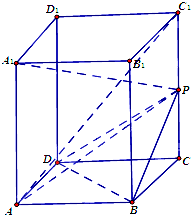如图，在直四棱柱ABCD-A1B1C1D1中，已知底面ABCD是边长为1的正方形，侧棱C1C垂直于底面ABCD，且C1C=2，点P是侧棱C1C的中点．
（1）求证：AC1∥平面PBD；
（2）求证：A1P⊥平面PBD；
（3）求三棱锥A1-BDC1的体积V．
已知：如图，△ABC中，AD⊥BC于D，CE⊥AB于E，AD、EC交于点F．求证
CD
AD
=
FD
BD
．
调查某桑场采桑员和辅助工患桑毛虫皮炎病的情况，结果如下表：
采桑 不采桑 合计
患者人数 18 12 30
健康人数 5 78 83
合计 23 90 113
利用2×2列联表的独立性检验估计，“患桑毛虫皮炎病与采桑”是否有关？认为两者有关系会犯错误的概率是多少？附表：
P（K≥k0） 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828
已知双曲线方程x2-y2=2，则过点P（1，0）和双曲线只有一个交点的直线有
 
条．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网