题目内容
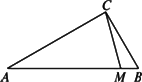
如图所示,Rt△ABC内接于圆,∠ABC=60°,PA是圆的切线,A为切点,PB交AC于E,交圆于D.若PA=AE,PD=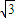 ,BD=
,BD=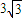 ,则AP= ,AC= .
,则AP= ,AC= .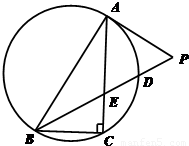
【答案】分析:由PDB为圆O的割线,PA为圆的切线,由切割线定理,结合PD=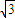 ,BD=3
,BD=3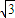 易得AP长;由∠ABC=60°结合弦切角定理易得△PAE为等边三角形,进而根据PE长求出AE长及ED,DB长,再根据相交弦定理可求出CE,进而得到答案.
易得AP长;由∠ABC=60°结合弦切角定理易得△PAE为等边三角形,进而根据PE长求出AE长及ED,DB长,再根据相交弦定理可求出CE,进而得到答案.
解答: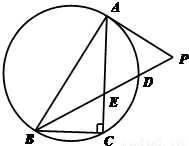 解:∵PD=
解:∵PD=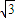 ,BD=3
,BD=3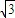 ,
,
∴PB=PD+BD=4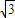 ,
,
由切割线定理得PA2=PD•PB=12
∴AP=2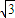 ,
,
又∵PE=PA
∴PE=2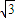
又∠PAC=∠ABC=60°
∴AE=2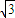
又由DE=PE-PD=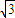
BE=BD-DE=2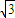 ,
,
由相交弦定理可得:
AE•CE=BE•ED=2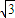 CE=6
CE=6
即CE=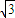
∴AC=AE+CE=3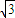 .
.
故答案: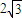 ;
;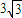 .
.
点评:本题考查的知识点是与圆相关的比例线段,根据已知条件求出与圆相关线段的长,构造方程组,求出未知线段是解答的关键.
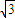 ,BD=3
,BD=3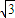 易得AP长;由∠ABC=60°结合弦切角定理易得△PAE为等边三角形,进而根据PE长求出AE长及ED,DB长,再根据相交弦定理可求出CE,进而得到答案.
易得AP长;由∠ABC=60°结合弦切角定理易得△PAE为等边三角形,进而根据PE长求出AE长及ED,DB长,再根据相交弦定理可求出CE,进而得到答案.解答:
 解:∵PD=
解:∵PD=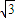 ,BD=3
,BD=3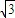 ,
,∴PB=PD+BD=4
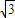 ,
,由切割线定理得PA2=PD•PB=12
∴AP=2
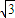 ,
,又∵PE=PA
∴PE=2
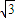
又∠PAC=∠ABC=60°
∴AE=2
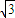
又由DE=PE-PD=
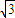
BE=BD-DE=2
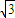 ,
,由相交弦定理可得:
AE•CE=BE•ED=2
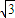 CE=6
CE=6即CE=
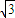
∴AC=AE+CE=3
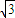 .
.故答案:
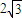 ;
;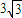 .
.点评:本题考查的知识点是与圆相关的比例线段,根据已知条件求出与圆相关线段的长,构造方程组,求出未知线段是解答的关键.

练习册系列答案
相关题目
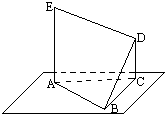
 如图所示,在Rt△ABC中,∠CAB=90°,AB=2,AC=
如图所示,在Rt△ABC中,∠CAB=90°,AB=2,AC=