题目内容
如图所示,斜边为AB的Rt△ABC,过A作PA⊥平面ABC,AE⊥PB,AF⊥PC,E,F分别为垂足.(1)求证:PB⊥平面AEF;
(2)若∠PBA=∠BAC=45°,求二面角A-PB-C的大小;
(3)若PA=AB=2,∠BPC=θ,求θ为何值时,S△AEF最大,最大值是多少?
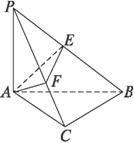
(1)证明:BC⊥平面PAC,再证AF⊥平面PBC,即可证PB⊥平面AEF.
(2)解:∠AEF是所求二面角的平面角,设AB=a,
∴AE=![]() a,AC=
a,AC=![]() a,PC=
a,PC=![]() a.
a.
又AF=![]() a,∴sin∠AEF=
a,∴sin∠AEF=![]() .∴∠AEF=arcsin
.∴∠AEF=arcsin![]() .
.
(3)解:由题意P,A,B,E是定点,C,F是动点,且F随C运动而运动.
∵C在平面ABC内沿以AB为直径的圆周上移动(不包括A,B两点),由PB⊥平面AEF,且∠AFE=90°,
∴F在过A而垂直于PB的平面内,在以AE为直径的圆周上移动(不包括A,E两点).
∴当AF=EF时,S△AEF最大,此时AE=![]() AB=
AB=![]() ,EF=
,EF=![]() AE=1.
AE=1.
在Rt△PEF中,PE=![]() PB=
PB=![]() AB=
AB=![]() ,tanθ=
,tanθ=![]() =
=![]() ,
,
∴θ=arctan![]() 时,S△AEF最大,最大值为
时,S△AEF最大,最大值为![]() AF·EF=
AF·EF=![]() .
.

练习册系列答案
相关题目
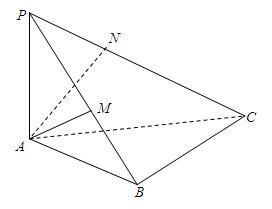 21、如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,AN⊥PC于N.
21、如图所示,在斜边为AB的Rt△ABC中,过A作PA⊥平面ABC,AM⊥PB于M,AN⊥PC于N.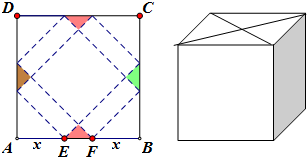 请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).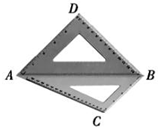 将一幅斜边长相等的直角三角板拼接成如图所示的空间图形,其中AD=BD=
将一幅斜边长相等的直角三角板拼接成如图所示的空间图形,其中AD=BD= (2013•南开区二模)如图所示,以直角三角形ABC的直角边AC为直径作⊙O,交斜边AB于点D,过点D作⊙O的切线,交BC边于点E.则
(2013•南开区二模)如图所示,以直角三角形ABC的直角边AC为直径作⊙O,交斜边AB于点D,过点D作⊙O的切线,交BC边于点E.则