题目内容
在四面体ABCD中,有如下结论:
①若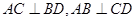 ,则
,则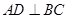 ;
;
②若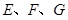 分别是
分别是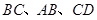 的中点,则
的中点,则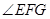 的大小等于异面直线
的大小等于异面直线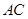 与
与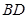 所成角的大小;
所成角的大小;
③若点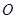 是四面体
是四面体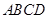 外接球的球心,则
外接球的球心,则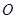 在面
在面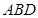 上的射影为
上的射影为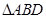 的外心;
的外心;
④若四个面是全等的三角形,则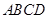 为正四面体.
为正四面体.
其中所有正确结论的序号是 .
①若
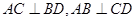 ,则
,则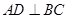 ;
;②若
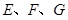 分别是
分别是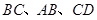 的中点,则
的中点,则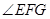 的大小等于异面直线
的大小等于异面直线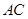 与
与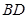 所成角的大小;
所成角的大小;③若点
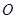 是四面体
是四面体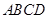 外接球的球心,则
外接球的球心,则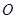 在面
在面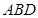 上的射影为
上的射影为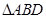 的外心;
的外心;④若四个面是全等的三角形,则
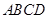 为正四面体.
为正四面体.其中所有正确结论的序号是 .
①③
试题分析:对于①,如图(1),作
 面
面 ,则有
,则有 ,而
,而 ,所以
,所以 面
面 ,所以
,所以 ,同理可证
,同理可证 ,故
,故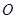 为三角形
为三角形 的垂心,所以
的垂心,所以 ,而
,而 ,所以
,所以 平面
平面 ,故
,故 ,命题正确;对于②,应该讲当
,命题正确;对于②,应该讲当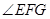 为锐角或直角时,
为锐角或直角时,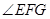 等于异面直线
等于异面直线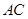 与
与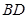 所成的角,当
所成的角,当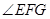 为钝角时,
为钝角时,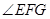 的补角才等于异面直线
的补角才等于异面直线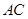 与
与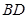 所成的角,命题不正确;对于③,根据球的性质:球心
所成的角,命题不正确;对于③,根据球的性质:球心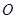 与小圆圆心(本题中相当于
与小圆圆心(本题中相当于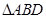 外接圆的圆心)相连垂直于小圆所在的平面,可知该命题正确;对于④,如下图(2),其中
外接圆的圆心)相连垂直于小圆所在的平面,可知该命题正确;对于④,如下图(2),其中 ,易知该三棱锥的四个面都是全等的三角形,但该三棱锥并不是正四面体.
,易知该三棱锥的四个面都是全等的三角形,但该三棱锥并不是正四面体.


练习册系列答案
相关题目
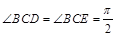 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.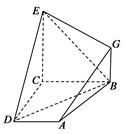
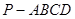 中,底面
中,底面 为矩形,
为矩形,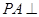 底面
底面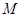 、
、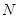 分别是
分别是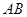 、
、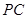 中点.
中点. 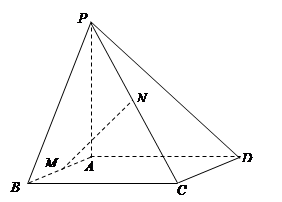
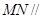 平面
平面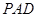 ;
;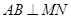 .
.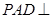 底面
底面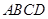 ,且△PAD为等腰直角三角形,
,且△PAD为等腰直角三角形,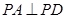 ,E、F分别为PC、BD的中点.
,E、F分别为PC、BD的中点.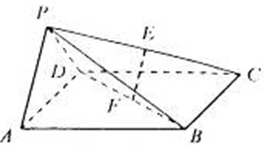
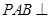 平面
平面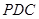 .
.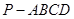 中,底面
中,底面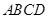 是边长为
是边长为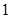 的正方形,
的正方形,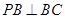 ,
,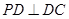 ,且
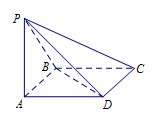
,且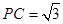 .
.
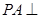 平面
平面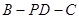 的余弦值;
的余弦值;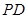 上是否存在一点
上是否存在一点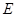 ,使直线
,使直线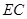 与平面
与平面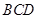 所成的角是
所成的角是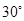 ?若存在,求
?若存在,求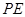 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.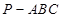 中,
中,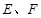 分别为
分别为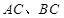 的中点.
的中点.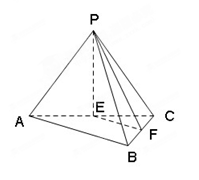
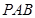 ;
;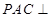 平面
平面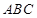 ,且
,且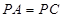 ,
,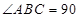 º,求证:平面
º,求证:平面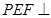 平面
平面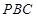
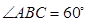 ,
,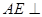 平面ABCD,
平面ABCD,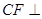 平面ABCD,
平面ABCD,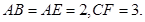
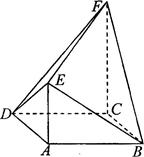
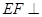 平面BDE;
平面BDE;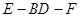 的大小.
的大小.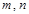 为两条不同直线,
为两条不同直线,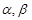 为两个不同平面,给出下列命题:
为两个不同平面,给出下列命题: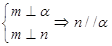 ②
②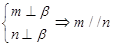
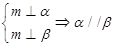 ④
④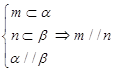
 是互不重合的直线,
是互不重合的直线, 是互不重合的平面,给出下列命题:
是互不重合的平面,给出下列命题: 则
则 或
或 ;
; 则
则 ;
; 不垂直于
不垂直于 ,则
,则 且
且 则
则
 ;
; 且
且 则
则 .
.