题目内容
△ABC中,点D、E、F分别为AB、BC、CA的中点,则 =
=
- A.

- B.
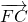
- C.
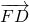
- D.

D
分析:本题考查的知识点是向量的减法及其几何意义,由D、E、F分别为AB、BC、CA的中点,我们易得 =
=
 =
=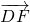 ,然后根据图形分析答案中的四个变量,易求出与
,然后根据图形分析答案中的四个变量,易求出与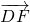 相等的向量,即可求出答案.
相等的向量,即可求出答案.
解答:如下图所示:

△ABC中,点D、E、F分别为AB、BC、CA的中点
则
=
 -
-

= (
( -
- )
)
=
 =
=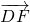 =
= .
.
故选D.
点评:向量加法的三角形法则,可理解为“首尾相接”,向量减法的三角形法则,可理解为“同起点,连终点,方向指被减.”
分析:本题考查的知识点是向量的减法及其几何意义,由D、E、F分别为AB、BC、CA的中点,我们易得
 =
=
 =
=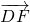 ,然后根据图形分析答案中的四个变量,易求出与
,然后根据图形分析答案中的四个变量,易求出与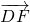 相等的向量,即可求出答案.
相等的向量,即可求出答案.解答:如下图所示:

△ABC中,点D、E、F分别为AB、BC、CA的中点
则

=

 -
-

=
 (
( -
- )
)=

 =
=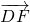 =
= .
.故选D.
点评:向量加法的三角形法则,可理解为“首尾相接”,向量减法的三角形法则,可理解为“同起点,连终点,方向指被减.”

练习册系列答案
相关题目
△ABC中,点D、E、F分别为AB、BC、CA的中点,则
-
=( )
| AF |
| DB |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在正△ABC中,点D,E分别在边AC,AB上,且AD=
如图,在正△ABC中,点D,E分别在边AC,AB上,且AD= 选修4-1:几何证明选讲如图,在正△ABC中,点D,E分别在边t上,且
选修4-1:几何证明选讲如图,在正△ABC中,点D,E分别在边t上,且