题目内容
如图,已知在△ABC中,点D.E分别在AB、AC上,且AD•AB=AE•AC,CD与BE相交于点O.
(I)求证:△AEB∽△ADC:
(II)求证:
=
.
(I)求证:△AEB∽△ADC:
(II)求证:
| BO |
| CO |
| DO |
| EO |
分析:利用三角形相似的判定与性质即可证明.
解答:证明:(I)∵AD•AB=AE•AC,
∴
=
,又∠A公用,
∴△AEB∽△ADC.
(II)∵△AEB∽△ADC,∴∠ABE=∠ACD,
又∠DOB=∠EOC,
∴△BOD∽△COE.
∴
=
.
∴
| AD |
| AC |
| AE |
| AB |
∴△AEB∽△ADC.
(II)∵△AEB∽△ADC,∴∠ABE=∠ACD,
又∠DOB=∠EOC,
∴△BOD∽△COE.
∴
| BO |
| CO |
| DO |
| EO |
点评:熟练掌握三角形相似的判定与性质及对顶角的性质是解题得到关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
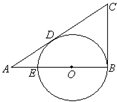
如图,已知在△ABC中,∠ACB=90°,CD⊥AB于D,AC=6,DB=5,则AD的长为( )

| A、3 | B、4 | C、5 | D、6 |
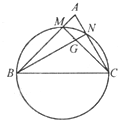 (2013•成都一模)如图,已知在△ABC中,BC=2,以BC为直径的圆分别交AB,AC于点M,N,MC与NB交于点G,若
(2013•成都一模)如图,已知在△ABC中,BC=2,以BC为直径的圆分别交AB,AC于点M,N,MC与NB交于点G,若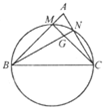 如图,已知在△ABC中,BC=2,以BC为直径的圆分别交AB,AC于点M,N,MC与NB交于点G,若
如图,已知在△ABC中,BC=2,以BC为直径的圆分别交AB,AC于点M,N,MC与NB交于点G,若