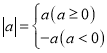题目内容
【题目】已知函数
.
（1）若函数
有两个不相等的正零点，求
的取值范围；
（2）若函数在
上的最小值为-3，求的值.
【答案】（1）
；（2）
.
【解析】试题分析: (1)将函数有两个不相等的正零点转化为对应的二次方程有两个不相等的正根,利用二次方程根的分布可得关于
的不等式组,解不等式组可得的取值范围;(2)先利用对称轴方程
与区间
之间的关系进行讨论,可得函数的最小值,再由最小值为
求出对应的值即可.
试题解析：（1）由函数
有两个不相等的正零点，可得对于方程
，有
，解得
.
（2）函数的图象的对称轴是，当
，即
时，函数在区间上单调递增，则
；当
，即
时，
；当
，即
时，函数在区间上单调递减，则
.故
.
当时，令
，无解；
当
时，令
，解得；
当时，令
，无解.
综上，.
练习册系列答案
相关题目
【题目】计划在某水库建一座至多安装3台发电机的水电站，过去50年的水文资料显示，水库年入流量
(年入流量：一年内上游来水与库区降水之和.单位：亿立方米）都在40以上.其中，不足80的年份有10年，不低于80且不超过120的年份有35年，超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率，并假设各年的年入流量相互独立.
（1）求未来4年中，至多1年的年入流量超过120的概率；
（2）水电站希望安装的发电机尽可能运行，但每年发电机最多可运行台数受年入流量
限制，并有如下关系:
年入流量 |
|
|
|
发电量最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行，则该台年利润为5000万元；若某台发电机未运行，则该台年亏损800万元，欲使水电站年总利润的均值达到最大，应安装发电机多少台？
