题目内容
9.下列各图中表示的对应法则是不是映射?为什么?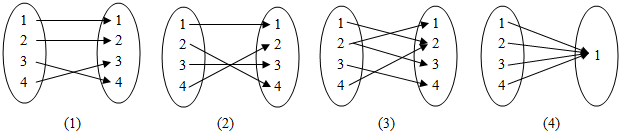
分析 本题考查的知识点是映射的定义,我们可以根据映射的定义:有非空集合P、M.当P中的每一个元素都能够在M中找到一个且只有一元素与之对应.根据映射的定义对四个对应逐一进行分析,即可得到答案.
解答 解:当A中的每一个元素都能够在B中找到一个且只有一元素与之对应的时候,那么就称这是集合A到集合B的一个映射.
(1)满足映射的定义,是映射;
(2)满足映射的定义,是映射;
(3)集合P中元素2,在集合M中有两个元素与之对应,不满足映射的定义,不是映射;
(4)满足映射的定义,是映射;
点评 根据映射成立的条件:有非空集合A、B.当A中的每一个元素都能够在B中找到一个且只有一元素与之对应的时候,那么就称这是集合A到集合B的一个映射. 只要符合对应中A中元素满足任意性,B中对应元素满足唯一性,即可判断该对应为映射.

练习册系列答案
相关题目
17.已知x>1,则xlnlnx-(lnx)lnx的值是( )
| A. | 正数 | B. | 零 | C. | 负数 | D. | 不能确定 |
19.若函数y=cos($\frac{π}{2}$+x),y=cos(2π-x)都是减函数,则x的集合是( )
| A. | {x|2kπ≤x≤$\frac{π}{2}$+2kπ,k∈Z} | B. | {x|kπ≤x≤$\frac{π}{2}$+kπ,k∈Z} | ||
| C. | {x|-$\frac{π}{2}$+2kπ≤x≤$\frac{π}{2}$+2kπ,k∈Z} | D. | {x|$\frac{π}{2}$+2kπ≤x≤$\frac{3}{2}$π+2kπ,k∈Z} |