题目内容
已知函数f（x）是二次函数，g（x）=2x+1，f[g（x）]=4x2+2x，f（x）的解析式为 ．
考点：函数解析式的求解及常用方法,二次函数的性质
专题：函数的性质及应用
分析：用待定系数法，设二次函数f（x）的解析式，代入f[g（x）]=4x2+2x中，可求得系数a、b、c，即f（x）的解析式；
解答：
解：设f（x）=ax2+bx+c（其中a≠0），
∵g（x）=2x+1
∴f[g（x）]=a（2x+1）2+b（2x+1）+c
=4ax2+（4a+2b）x+a+b+c=4x2+2x，
∴
，
解得：
∴f（x）的解析式为f（x）=x2-x，
故答案为：f（x）=x2-x
∵g（x）=2x+1
∴f[g（x）]=a（2x+1）2+b（2x+1）+c
=4ax2+（4a+2b）x+a+b+c=4x2+2x，
∴
|
解得：
|
∴f（x）的解析式为f（x）=x2-x，
故答案为：f（x）=x2-x
点评：本题考查的知识点是函数解析式的求解及常用方法，熟练掌握待定系数法求函数解析式的方法和步骤是解答的关键．
练习册系列答案
相关题目
已知圆柱的侧面展开图是边长分别为2a，a的矩形，则该圆柱的体积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
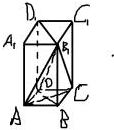如图，在直棱柱ABCD-A1B1C1D1中，AA1=4，底面是边长为2的菱形，且∠BAD=60°．