题目内容
6.若钝角三角形ABC三边长分别是a,a+1,a+2,则a的取值范围(1,3).分析 由已知利用大边对大角,余弦定理可得$\frac{{a}^{2}-2a-3}{2a(a+1)}$<0,解不等式组可得:-1<a<3,利用三角形两边之和大于第三边可解得:a>1,即可得解.
解答 解:∵钝角三角形三边长为a,a+1,a+2,
∴a+2对的角为钝角,设为α,
∴cosα=$\frac{{a}^{2}+(a+1)^{2}-(a+2)^{2}}{2a(a+1)}$=$\frac{{a}^{2}-2a-3}{2a(a+1)}$<0,
解得:-1<a<3,
由a+a+1>a+2,解得:a>1,
则a的取值范围为(1,3).
故答案为:(1,3)
点评 本题主要考查了大边对大角,余弦定理,不等式组的解法,三角形两边之和大于第三边等知识在解三角形中的综合应用,考查了转化思想,属于中档题.

练习册系列答案
相关题目
17.已知直线m,n与平面α,β,下列四个命题为真命题的是( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若m⊥α,n⊥α,则m∥n | ||
| C. | 若m∥α,n∥α,β∥α,则m∥n | D. | 若m∥n,m∥α,则n∥α |
14.某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金不超过54万元,假设种植黄瓜和韭菜的产量、成本和售价如表:
则一年的种植总利润(总利润=总销售收入-总种植成本最大值为45万元.
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 5吨 | 0.9万元 | 0.3万元 |
18.从全体3位正整数中任取一数,则此数以2为底的对数也是正整数的概率为( )
| A. | $\frac{1}{225}$ | B. | $\frac{1}{300}$ | C. | $\frac{1}{450}$ | D. | 以上全不对 |
15.下列函数在区间(0,+∞)内单调递减的是( )
| A. | y=x3 | B. | y=$\frac{1}{x-1}$ | C. | y=log2$\frac{1}{x}$ | D. | y=-tanx |
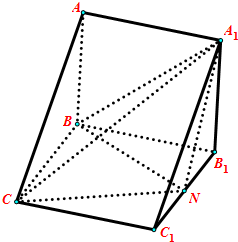 在直棱柱ABC-A1B1C1中,平面A1BC⊥平面A1ABB1,且AA1=AB=BC=2.N为B1C1中点.
在直棱柱ABC-A1B1C1中,平面A1BC⊥平面A1ABB1,且AA1=AB=BC=2.N为B1C1中点.