题目内容
某个与自然数有关的命题:如果当n=k(k∈N*)时,命题成立,则可以推出n=k+1时,该命题也成立.现已知n=6时命题不成立
- A.当n=5时命题不成立
- B.当n=7时命题不成立
- C.当n=5时命题成立
- D.当n=8时命题成立
A
分析:由归纳法的性质,我们由P(n)对n=k成立,则它对n=k+1也成立,由此类推,对n>k的任意整数均成立,结合逆否命题同真同假的原理,当P(n)对n=k不成立时,则它对n=k-1也不成立,由此类推,对n<k的任意正整数均不成立,由此不难得到答案.
解答:由题意可知,根据互为逆否命题的等价性,可得n=5时命题不成立(否则n=6也成立).
故选A.
点评:本题考查的知识点是数学归纳法,考查互为逆否命题的等价性,属于基础题.
分析:由归纳法的性质,我们由P(n)对n=k成立,则它对n=k+1也成立,由此类推,对n>k的任意整数均成立,结合逆否命题同真同假的原理,当P(n)对n=k不成立时,则它对n=k-1也不成立,由此类推,对n<k的任意正整数均不成立,由此不难得到答案.
解答:由题意可知,根据互为逆否命题的等价性,可得n=5时命题不成立(否则n=6也成立).
故选A.
点评:本题考查的知识点是数学归纳法,考查互为逆否命题的等价性,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
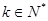 )时,命题成立,则可以推出n=k+1时,该命题也成立.现已知n=6时命题不成立( ).
)时,命题成立,则可以推出n=k+1时,该命题也成立.现已知n=6时命题不成立( ).