Question

已知a>1，f(log_a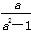x)＝·(x－)．

(1)求f(x)；

(2)判断并证明f(x)的单调性；

(3)若f(1－m)＋f(2m)<0，求m的取值范围．

Answer 1

[解析]　(1)设t＝log_ax，则x＝a^t，

则f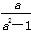(t)＝(a^t－)，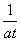

∴f(x)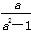＝(a^x－a^－x)(x∈R)．

(2)设x₁<x₂，则f(x₁)－f(x₂)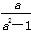＝(ax₁－a－x₁)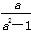－(ax₂－a－x₂)

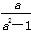＝[(ax₁－ax₂)＋(a－x₂－a－x₁)]

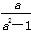＝(ax₁－ax₂)(1＋)．

∵a>1，∴ax₁<ax₂，则有ax₁－ax₂<0.

而>0,1＋>0，

∴f(x₁)－f(x₂)<0，即f(x₁)<f(x₂)．

∴函数f(x)为R上的增函数．

(3)∵f(－x)＝(a^－x－a^x)

＝－(a^x－a^－x)＝－f(x)，

∴f(x)为奇函数．

∵f(1－m)＋f(2m)<0，

∴f(1－m)<－f(2m)＝f(－2m)．

∵f(x)在R上是增函数，

∴1－m<－2m.

解得m<－1.

故m的取值范围是(－∞，－1)．