题目内容
10.已知sinθ=$\frac{4}{5}$,且θ∈($\frac{π}{2}$,π),求sin(θ-$\frac{π}{6}$)和cos(θ+$\frac{π}{6}$)的值.分析 利用同角三角函数的基本关系式以及两角和与差的三角函数求解即可.
解答 解:sinθ=$\frac{4}{5}$,且θ∈($\frac{π}{2}$,π),cosθ=-$\frac{3}{5}$.
sin(θ-$\frac{π}{6}$)=sinθcos$\frac{π}{6}$-cosθsin$\frac{π}{6}$=$\frac{4}{5}×\frac{\sqrt{3}}{2}+\frac{3}{5}×\frac{1}{2}$=$\frac{3+4\sqrt{3}}{10}$.
cos(θ+$\frac{π}{6}$)=cosθcos$\frac{π}{6}$-sinθsin$\frac{π}{6}$=$-\frac{3}{5}×\frac{\sqrt{3}}{2}-\frac{4}{5}×\frac{1}{2}$=-$\frac{4+3\sqrt{3}}{10}$.
点评 本题考查两角和与差的三角函数,同角三角函数的基本关系式的应用,考查计算能力.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
5.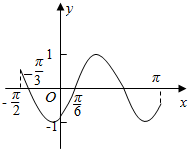 若函数y=sin(ωx-φ)(ω>0,|φ|<π)在区间$[{-\frac{π}{2},π}]$的简图如图所示,则ω,φ的值分别是( )
若函数y=sin(ωx-φ)(ω>0,|φ|<π)在区间$[{-\frac{π}{2},π}]$的简图如图所示,则ω,φ的值分别是( )
 若函数y=sin(ωx-φ)(ω>0,|φ|<π)在区间$[{-\frac{π}{2},π}]$的简图如图所示,则ω,φ的值分别是( )
若函数y=sin(ωx-φ)(ω>0,|φ|<π)在区间$[{-\frac{π}{2},π}]$的简图如图所示,则ω,φ的值分别是( )| A. | $ω=2,φ=\frac{π}{3}$ | B. | $ω=2,φ=-\frac{2π}{3}$ | C. | $ω=\frac{1}{2},φ=\frac{π}{3}$ | D. | $ω=\frac{1}{2},φ=-\frac{2π}{3}$ |
 如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)经过点A(0,-1),且离心率为$\frac{{\sqrt{2}}}{2}$.求椭圆E的方程.
如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)经过点A(0,-1),且离心率为$\frac{{\sqrt{2}}}{2}$.求椭圆E的方程.