题目内容
14.在平面直角坐标内A,B两点满足:①点A,B都在函数y=f(x)的图象上;
②点A,B关于原点对称,则称A,B为函数y=f(x)的一个“黄金点对”.
则函数f(x)=$\left\{\begin{array}{l}{|x+4|,x≤0}\\{-\frac{1}{x},x>0}\end{array}\right.$的“黄金点对”的个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 根据题意:“黄金点对”,可知,欲求f(x)的“黄金点对”,只须作出函数y=-$\frac{1}{x}$(x>0)的图象关于原点对称的图象,看它与函数y=|x+4|,x≤0的图象的交点个数即可.
解答 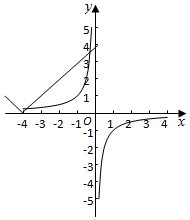 解:根据题意:“黄金点对”,可知,
解:根据题意:“黄金点对”,可知,
作出函数y=-$\frac{1}{x}$(x>0)的图象关于原点对称的图象,
同一坐标系里作出函数y=|x+4|,x≤0的图象如右图:
观察图象可得,它们在x≤0时的交点个数是3.
即f(x)的“黄金点对”有:3个.
故选:D.
点评 本题主要考查了奇偶函数图象的对称性,以及数形结合的思想,属于基础题.解答的关键在于对“黄金点对”的正确理解,合理地利用图象法解决.

练习册系列答案
相关题目
4.已知直线a,b都与平面α相交,则a,b的位置关系是( )
| A. | 平行 | B. | 相交 | C. | 异面 | D. | 以上都有可能 |
5.已知函数$y={log_a}({x^2}-ax+\frac{1}{2})$,对任意的x1,x2∈[1,+∞),且x1≠x2时,满足$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}>0$,则实数a的取值范围是( )
| A. | $(1,\frac{3}{2})$ | B. | $({\frac{3}{2},+∞}]$ | C. | (1,2] | D. | [2,+∞) |
9.有5名学生、2名老师站成一行照相,2名老师不能相邻的排法有( )
| A. | ${A}_{5}^{2}$${A}_{2}^{2}$ | B. | ${A}_{7}^{7}$-${A}_{2}^{2}$${A}_{6}^{6}$ | ||
| C. | ${A}_{7}^{7}$-${A}_{6}^{6}$ | D. | ${C}_{10}^{8}$0.820.28 |
19.下列结论不正确的是( )
| A. | 若y=ln3,则y′=0 | B. | 若y=-$\sqrt{x}$,则y′=-$\frac{1}{2\sqrt{x}}$ | ||
| C. | 若y=$\frac{1}{\sqrt{x}}$,则y′=-$\frac{1}{2\sqrt{x}}$ | D. | 若y=3x,则y′=3 |
4.两圆C1:x2+y2=4与C2:x2+y2-2x-1=0的位置关系是( )
| A. | 相外切 | B. | 相内切 | C. | 相交 | D. | 外离 |