题目内容
9．已知函数f（x）=$\frac{{x}^{2}}{\sqrt{4-{x}^{2}}}$，函数g（x）=$\sqrt{4-{x}^{2}}$．作出函数F（x）=$\left\{\begin{array}{l}{f（x）•g（x），（x≤0）}\\{x，（0＜x≤2）}\end{array}\right.$的图象．分析 化简可得F（x）=$\left\{\begin{array}{l}{{x}^{2}，-2＜x≤0}\\{x，0＜x≤2}\end{array}\right.$，从而作其函数的图象即可．
解答 解：函数f（x）=$\frac{{x}^{2}}{\sqrt{4-{x}^{2}}}$的定义域为（-2，2），
函数g（x）=$\sqrt{4-{x}^{2}}$的定义域为[-2，2]，
f（x）•g（x）=x2，
故F（x）=$\left\{\begin{array}{l}{{x}^{2}，-2＜x≤0}\\{x，0＜x≤2}\end{array}\right.$，
故作函数F（x）=$\left\{\begin{array}{l}{{x}^{2}，-2＜x≤0}\\{x，0＜x≤2}\end{array}\right.$的图象如下，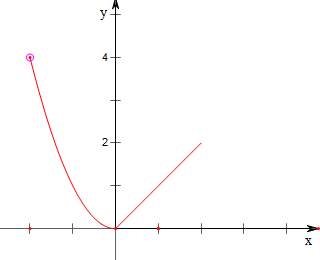
．
点评 本题考查了函数的化简与函数的图象的作法．
练习册系列答案
相关题目
4．已知函数f（x-$\frac{π}{6}$）=sin2x，则f（$\frac{π}{2}$）等于（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |