题目内容
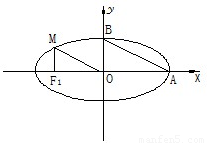
如图,从椭圆
 上一点
上一点 向
向 轴作垂线,恰好通过椭圆的左焦点
轴作垂线,恰好通过椭圆的左焦点 ,且它的长轴端点
,且它的长轴端点 及短轴端点
及短轴端点 的连线
的连线 平行于
平行于 ,
,
(1)求椭圆的离心率;
(2)设 是椭圆上任意一点,
是椭圆上任意一点, 是右焦点,求
是右焦点,求 的取值范围;
的取值范围;
(3)设 是椭圆上一点,当
是椭圆上一点,当 时,延长
时,延长 与椭圆交于另一点
与椭圆交于另一点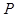 ,若
,若 的面积为
的面积为 ,求此时的椭圆方程。(10分)
,求此时的椭圆方程。(10分)

【答案】
解:(1) ,
, ,因为
,因为 ,
, ,得
,得 ,
,
则 。
(2分)
。
(2分)
(2)在三角形 中,由余弦定理得:
中,由余弦定理得:



=




 ,又因为
,又因为 ,所以
,所以 ,即
,即 。 (5分 )
。 (5分 )
(3)由(1)知, ,故设椭圆方程为
,故设椭圆方程为 ,
, ,因为
,因为 所以
所以 ,故直线
,故直线 的方程为
的方程为 , (6分)
, (6分)
联立方程组
 ,整理得
,整理得
 ,记
,记

 ,设
,设 ,由韦达定理得:
,由韦达定理得: ,
, ,
,


 =
=
 (8分)
(8分)
又点 到
到 的距离
的距离
 ,所以
,所以

 。
。
所以 ,故椭圆方程为
,故椭圆方程为 (10分)
(10分)
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,从椭圆E:
如图,从椭圆E: 如图:从椭圆
如图:从椭圆 如图:从椭圆
如图:从椭圆 上一点M向x轴作垂线,恰好通过椭圆的左焦点F1(-c,0),且
上一点M向x轴作垂线,恰好通过椭圆的左焦点F1(-c,0),且 ∥
∥ ,则a,b,c必满足________.
,则a,b,c必满足________.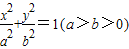 上一点M向x轴作垂线,恰好通过椭圆的左焦点F1(-c,0),且
上一点M向x轴作垂线,恰好通过椭圆的左焦点F1(-c,0),且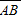 ∥
∥ ,则a,b,c必满足 .
,则a,b,c必满足 .