题目内容

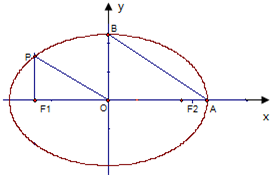如图，从椭圆E：
x2
a2
+
y2
b2
=1(a＞b＞0)上一点P向x轴作垂线，垂足恰为左焦点F1，又点A是椭圆与x轴正半轴的交点，点B是椭圆与y轴正半轴的交点，且AB∥OP，|F1A|=
10
+
5
，
（1）求椭圆E的方程．
（2）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点C，D，且
OC
⊥
OD
？若存在，写出该圆的方程，并求|CD|的取值范围；若不存在，说明理由．
分析：（1）易求点P坐标，由kOP=kAB，由斜率公式可得b，c关系，进而可得a，c关系，由|F1A|=
10
+
5
得关于a，c的方程，可求得c，进而可得a，b；
（2）假设存符合题意的圆，切线与椭圆的交点为C（x1，y1），D（x2，y2），当该圆的切线不垂直x轴时，设其方程为y=kx+m，与椭圆方程联立消掉y可得x的二次方程，则△＞0①，由
OC
⊥
OD
，得x1x2+y1y2=0，代入韦达定理可得k，m的关系式②，由①②可求得m的范围，根据直线与圆相切可求得半径r，圆的方程，当切线斜率不存在时，求出切线方程、交点坐标可检验条件；当切线斜率不存在时易求|CD|；当切线存在斜率时，由弦长公式可用k表示出|CD|，再分k=0，k≠0两种情况求得其范围；
解答：解：（1）由题意可求点P的坐标为(-c，
b2
a
)，由AB∥OP得，
kOP=kAB⇒-
b2
ac
=-
b
a
⇒b=c，a=
2
c
|F1A|=a+c=(1+
2
)c=
10
+
5
⇒c=
5

∴a=
10
，b=
5
，
椭圆E的方程为
x2
10
+
y2
5
=1；
（2）假设存符合题意的圆，切线与椭圆的交点为C（x1，y1），D（x2，y2），
当该圆的切线不垂直x轴时，设其方程为y=kx+m，
由方程组
y=kx+m
x2
10
+
y2
5
=1
，得x2+2（kx+m）2=10，即（1+2k2）x2+4kmx+2m2-10=0，
则△=16k2m2-4（1+2k2）（2m2-10）=8（10k2-m2+5）＞0，即10k2-m2+5＞0，
x1+x2=-
4km
1+2k2
x1x2=
2m2-10
1+2k2
，
∴y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=
k2(2m2-10)
1+2k2
-
4k2m2
1+2k2
+m2=
m2-10k2
1+2k2
，
要使
OC
⊥
OD
，需使x1x2+y1y2=0，即
2m2-10
1+2k2
+
m2-10k2
1+2k2
=0，
∴3m2-10k2-10=0，∴k2=
3m2-10
10
≥0，
又10k2-m2+5＞0，∴
2m2＞5
3m2≥10
，
∴m2≥
10
3
，即m≥
30
3
或m≤-
30
3
，
∵直线y=kx+m为圆心在原点的圆的一条切线，
∴圆的半径为r=
|m|
1+k2
，r2=
m2
1+k2
=
m2
1+
3m2-10
10
=
10
3
，
所求的圆为x2+y2=
10
3
，
此时圆的切线y=kx+m都满足m≥
30
3
或m≤-
30
3
；
而当切线的斜率不存在时，切线为x=±
30
3
，与椭圆
x2
10
+
y2
5
=1的两个交点为(
30
3
，±
30
3
)或(-
30
3
，±
30
3
)，满足
OC
⊥
OD
；
综上所述，存在圆心在原点的圆x2+y2=
10
3
，使得该圆的任意一条切线与椭圆E恒有两个交点C，D，且
OC
⊥
OD
．
∵
x1+x2=-
4km
1+2k2
x1x2=
2m2-10
1+2k2
，
∴(x1-x2)2=(x1+x2)2-4x1x2=(-
4km
1+2k2
)2-4×
2m2-10
1+2k2
=
8(10k2-m2+5)
(1+2k2)2
，
∴|CD|=
1+k2
|x1-x2|=
1+k2
(x1+x2)2-4x1x2
=
40
3
•
4k4+5k2+1
4k4+4k2+1
=
40
3
(1+
k2
4k4+4k2+1
)
，
①当k≠0时，|CD|=
40
3
(1+
1
4k2+
1
k2
+4
)
，
∵4k2+
1
k2
+4≥8，∴0＜
1
4k2+
1
k2
+4
≤
1
8
，
∴
40
3
＜
40
3
[1+
1
4k2+
1
k2
+4
]≤15，
∴
2
30
3
＜|CD|≤
15
，当且仅当k=±
2
2
时取”=”．
②当k=0时，易求|CD|=
2
30
3
；
③当CD的斜率不存在时，两个交点为(
30
3
，±
30
3
)或(-
30
3
，±
30
3
)，∴此时|CD|=
2
30
3
；
综上所述，|CD|的取值范围为
2
30
3
≤|CD|≤
15
，即：|CD|∈[
2
30
3
，
15
]．
点评：本题考查直线与椭圆的位置关系、椭圆标准方程的求解，考查分类讨论思想、函数思想，考查学生综合运用所学知识分析问题解决问题的能力，本题综合性强，运算量大，能力要求较高．
练习册系列答案
相关题目
精英家教网如图，过椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）上的动点M引圆O：x2+y2=b2的两条切线MA，MB，其中A，B分别为切点，，若椭圆上存在点M，使∠BMA=
π
2
，则该椭圆的离心率为
 
．
已知椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
3
2
，其长轴长与短轴长的和等于6．
（1）求椭圆E的方程；
（2）如图，设椭圆E的上、下顶点分别为A1、A2，P是椭圆上异于A1、A2的任意一点，直线PA1、PA2分别交x轴于点N、M，若直线OT与过点M、N的圆G相切，切点为T．证明：线段OT的长为定值．
如图，从椭圆
x2
a2
+
y2
b2
=1（a＞b＞o）上一点P向x轴作垂线，垂足恰好为左焦点F1，又点A是椭圆与x轴正半轴的交点，点B是椭圆与y轴正半轴的交点，且AB∥OP，则椭圆的离心率e=
2
2
2
2
．
如图：从椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)上一点M向x轴作垂线，恰好通过椭圆的左焦点F1（-c，0），且
.
AB
∥
.
OM
，则a，b，c必满足
b=c=
2
2
a
b=c=
2
2
a
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网