题目内容
如图:从椭圆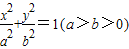 上一点M向x轴作垂线,恰好通过椭圆的左焦点F1(-c,0),且
上一点M向x轴作垂线,恰好通过椭圆的左焦点F1(-c,0),且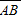 ∥
∥ ,则a,b,c必满足 .
,则a,b,c必满足 .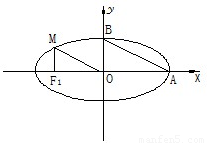
【答案】分析:根据MF1⊥x轴算出|MF1|= ,由
,由 ∥
∥ 得到△ABO∽△OMF1,利用比例线段得出b=c,再结合a2=b2+c2算出b=c=
得到△ABO∽△OMF1,利用比例线段得出b=c,再结合a2=b2+c2算出b=c= ,从而得到本题的答案.
,从而得到本题的答案.
解答:解:∵MF1⊥x轴,∴设M(-c,y),代入椭圆方程可得 ,
,
因此y= (舍负),可得|MF1|=
(舍负),可得|MF1|=
∵ ∥
∥ ,
,
∴△ABO∽△OMF1,可得 ,即
,即
解之得b=c,结合a2=b2+c2得b=c=
∴椭圆的离心率e=
故答案为:b=c=
点评:本题给出椭圆通径的一端与原点连线平行于右顶点、上顶点的连线,求a、b、c满足的关系式,着重考查了椭圆的标准方程与简单几何性质等知识,属于基础题.
 ,由
,由 ∥
∥ 得到△ABO∽△OMF1,利用比例线段得出b=c,再结合a2=b2+c2算出b=c=
得到△ABO∽△OMF1,利用比例线段得出b=c,再结合a2=b2+c2算出b=c= ,从而得到本题的答案.
,从而得到本题的答案.解答:解:∵MF1⊥x轴,∴设M(-c,y),代入椭圆方程可得
 ,
,因此y=
 (舍负),可得|MF1|=
(舍负),可得|MF1|=
∵
 ∥
∥ ,
,∴△ABO∽△OMF1,可得
 ,即
,即
解之得b=c,结合a2=b2+c2得b=c=

∴椭圆的离心率e=

故答案为:b=c=

点评:本题给出椭圆通径的一端与原点连线平行于右顶点、上顶点的连线,求a、b、c满足的关系式,着重考查了椭圆的标准方程与简单几何性质等知识,属于基础题.

练习册系列答案
相关题目
 上一点M向
上一点M向 轴作垂线,恰好通过椭圆的左焦点
轴作垂线,恰好通过椭圆的左焦点 ,且它的长轴端点A及短轴端点B的连线
,且它的长轴端点A及短轴端点B的连线 .
.
 是右焦点,
是右焦点, 的取值范围;
的取值范围;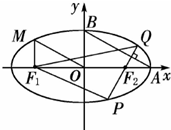 (普通班)如图所示,从椭圆
(普通班)如图所示,从椭圆 上一点M向x轴作垂线,恰好通过椭
上一点M向x轴作垂线,恰好通过椭 如图:从椭圆
如图:从椭圆 ∥
∥ ,则a,b,c必满足________.
,则a,b,c必满足________.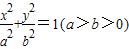 上一点M向x轴作垂线,恰好通过椭
上一点M向x轴作垂线,恰好通过椭