题目内容
已知a＞2，求证：log（a-1）a＞loga（a+1）
证明（法一）：∵
=
．
因为a＞2，所以，loga（a-1）＞0，loga（a+1）＞0，
所以，loga（a-1）•loga（a+1）
=
所以，log（a-1）a-loga（a+1）＞0，命题得证．
证明2：因为a＞2，所以，loga（a-1）＞0，loga（a+1）＞0，
所以，
由法1可知：loga（a-1）•loga（a+1）
=
∴
＞1．
故命题得证
分析：（法一）利用作差法：只要证明=＞0即可
（法二）作商法：只要证明＞1即可
点评：本题主要考查了不等式的证明方法的常用方法：作差证明差大于0，作商证明商大于1．
=
．因为a＞2，所以，loga（a-1）＞0，loga（a+1）＞0，
所以，loga（a-1）•loga（a+1）
=
所以，log（a-1）a-loga（a+1）＞0，命题得证．
证明2：因为a＞2，所以，loga（a-1）＞0，loga（a+1）＞0，
所以，
由法1可知：loga（a-1）•loga（a+1）
=
∴
＞1．故命题得证
分析：（法一）利用作差法：只要证明
=＞0即可（法二）作商法：只要证明
＞1即可点评：本题主要考查了不等式的证明方法的常用方法：作差证明差大于0，作商证明商大于1．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
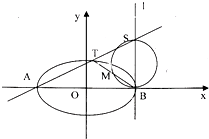已知椭圆C方程为
A．选修4-1：几何证明选讲
（2009•湖北模拟）已知A（-1，0）、B（3，0），M、N是圆O：x2+y2=1上的两个动点，且M、N关于x轴对称，直线AM与BN交于P点．