Question

已知椭圆C方程为

x2

a2

+y2=1，过右焦点斜率为1的直线到原点的距离为

2

2

．
（1）求椭圆方程．
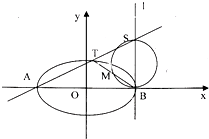
（2）已知A、B方程为椭圆的左右两个顶点，T为椭圆在第一象限内的一点，l为点B且垂直x轴的直线，点S为直线AT与直线l的交点，点M为以SB为直径的圆与直线TB的另一个交点，求证：

TB

-

SM

=

TB

-

SO

．

Answer 1

分析：（1）写出过右焦点斜率为1的直线方程，由点到直线的距离公式求出原点到该直线的距离由距离等于

2

2

求出c的值，则a可求，所以椭圆方程可求；
（2）设出直线AT的方程及点T的坐标，把直线方程和椭圆方程联立后化为关于x的一元二次方程，利用根与系数关系得到T点坐标，求出向量

BT

的坐标，由AT方程和直线x=

2

得到S的坐标，因为

SO

•

BT

=0，而BT⊥SM，所以得到O，M，S三点共线，从而得到

TB

-

SM

=

TB

-

SO

．

解答：解：解：（1）设右焦点为（c，0），则过右焦点斜率为1的直线方程为：y=x-c
则原点到直线的距离d=

|c|

2

=

2

2

∴c=1，a=

2

∴方程为

x2

2

+y2=1；
（2）设直线AT方程为：y=k（x+

2

）（k＞0），设点T（x₁，y₁），
联立

x2 2 +y2=1 y=k(x+ 2 )

，得(1+2k2)x2+4

2

k2x+4k2-2=0．
∵x1x2=

4k2-2

1+2k2

，又∵A（-

2

，0），
∴x1=

2 -2 2 k2

1+2k2

，y1=

2 2 k

1+2k2

．
又∵B（

2

，0），∴

BT

=(

-4 2 k2

1+2k2

，

2 2 k

1+2k2

)．
又∵S点的横坐标为

2

，
∴S点的坐标为(

2

，2

2

k)．
∴

SO

=(-

2

，-2

2

k)．
∴

SO

•

BT

=

8k2-8k2

1+2k2

=0．
即BT⊥SO，又∵BT⊥SM，
∴O，M，S三点共线，
所以

SM

=

SO

，
所以

TB

-

SM

=

TB

-

SO

．

点评：本题考查了椭圆的标准方程，考查了直线与圆锥曲线的关系，考查了数学转化思想方法，训练了利用平面向量解决有关问题，考查了学生的运算能力，是难题．