题目内容
数列1，（1+2），（1+2+22），…，（1+2+22+…+2n-1）…的前n项和为（ ）A．2n-1
B．n•2n-n
C．2n+1-n
D．2n+1-2-n
【答案】分析：由1+2+22+…+2n-1=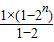
=2n-1可知，数列的前n项和为：（21-1）+（22-1）+（23-1）+…+（2n-1）=21+22+23+…+2n-n=
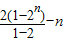=2n+1-2-n
解答：解：∵1+2+22+…+2n-1=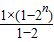
=2n-1
∴数列的前n项和为：1+（1+2）+（1+2+22）+…+（1+2+22+…+2n-1）
=（21-1）+（22-1）+（23-1）+…+（2n-1）
=21+22+23+…+2n-n
=
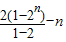=2n+1-2-n
故选D
点评：本题为数列的求和问题，求出数列的通项公式并应用到数列中是解决问题的关键，属中档题．
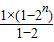=2n-1可知，数列的前n项和为：（21-1）+（22-1）+（23-1）+…+（2n-1）=21+22+23+…+2n-n=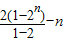=2n+1-2-n解答：解：∵1+2+22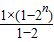+…+2n-1=
=2n-1∴数列的前n项和为：1+（1+2）+（1+2+22）+…+（1+2+22+…+2n-1）
=（21-1）+（22-1）+（23-1）+…+（2n-1）
=21+22+23+…+2n-n
=
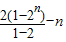=2n+1-2-n故选D
点评：本题为数列的求和问题，求出数列的通项公式并应用到数列中是解决问题的关键，属中档题．
练习册系列答案
发散思维新课堂系列答案
相关题目