题目内容
设数列1，（1+2），…，（1+2+…+2n-1），…的前n项和为Sn，则Sn等于
- A.2n
- B.2n-n
- C.2n+1-n
- D.2n+1-n-2
D
分析：先通过题意可知数列的每一项实际是由等比数列的和组成的，利用等比数列的求和公式求得数列的通项公式，进而利用等比数列和等差数列的求和公式求得问题的答案．
解答：依题意可知数列的每一项是由等比数列的和构成的，设为Tn，
则Tn=
=2n-1
∴数列是由等比数列和等差数列构成的，
则Sn=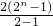
-n=2n+1-n-2
故选 D
点评：本题主要考查了数列的求和，求数列的通项公式等问题．解题的关键是求得数列的通项公式，从通项公式中发现规律．
分析：先通过题意可知数列的每一项实际是由等比数列的和组成的，利用等比数列的求和公式求得数列的通项公式，进而利用等比数列和等差数列的求和公式求得问题的答案．
解答：依题意可知数列的每一项是由等比数列的和构成的，设为Tn，
则Tn=
=2n-1∴数列是由等比数列和等差数列构成的，
则Sn=
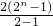-n=2n+1-n-2故选 D
点评：本题主要考查了数列的求和，求数列的通项公式等问题．解题的关键是求得数列的通项公式，从通项公式中发现规律．
练习册系列答案
相关题目
设数列1，（1+2），…，（1+2+…+2n-1），…的前n项和为Sn，则Sn等于（ ）
| A、2n | B、2n-n | C、2n+1-n | D、2n+1-n-2 |