题目内容
已知P是椭圆2x2+3y2=6上的点，则P到该椭圆的一个焦点的最短距离是 ．
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：首先，根据题意，即求a-c的值，将椭圆的方程化为标准方程后易得．
解答：
解：∵椭圆2x2+3y2=6，
∴
+
=1，
∴a=
，b=
，c=1，
∴P到该椭圆的一个焦点的最短距离是：a-c=
-1．
故答案为：
-1．
∴
| x2 |
| 3 |
| y2 |
| 2 |
∴a=
| 3 |
| 2 |
∴P到该椭圆的一个焦点的最短距离是：a-c=
| 3 |
故答案为：
| 3 |
点评：本题重点考查了椭圆的几何性质、椭圆的标准方程等知识，属于基础题．
练习册系列答案
相关题目
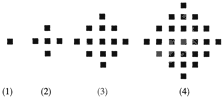某少数民族的刺绣有着悠久的历史，下图（1）、（2）、（3）、（4）为她们刺绣最简单的四个图案，这些图案都由小正方形构成，小正方形数越多刺绣越漂亮，现按同样的规律刺绣（小正方形的摆放规律相同），设第n个图形包含f（n）个小正方形．
已知函数f（x）=ax3+bx2+cx在点x0处取得极小值，其导函数y=f'（x）的图象经过点（1，0），（2，0），如图所示．则x0=