题目内容
在平面直角坐标系中,定义d(P,Q)=|x1-x2|+|y1-y2|为两点P(x1,y1),Q(x2,y2)之间的“折线距离”,在这个定义下,给出下列命题:
①到原点的“折线距离”等于1的点的集合是一个圆;
②到原点的“折线距离”小于等于2的点构成的区域面积为8;
③到M(0,-2),N(0,2)两点的“折线距离”相等的点的轨迹方程是y=0;
④直线y=x+1上的点到N(0,2)的“折线距离”的最小值为1.
其中真命题有( )
①到原点的“折线距离”等于1的点的集合是一个圆;
②到原点的“折线距离”小于等于2的点构成的区域面积为8;
③到M(0,-2),N(0,2)两点的“折线距离”相等的点的轨迹方程是y=0;
④直线y=x+1上的点到N(0,2)的“折线距离”的最小值为1.
其中真命题有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:进行简单的合情推理
专题:推理和证明
分析:先根据折线距离的定义分别表示出所求的集合,然后根据集合中绝对值的性质进行判定即可.
解答:
解:对于①到原点的“折线距离”等于1的点的集合{(x,y)||x|+|y|=1},是一个正方形故①错误;
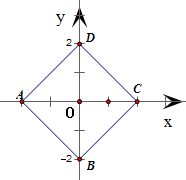
对于②根据题意,到坐标原点O的“折线距离”小于等于2的点P(x,y)满足等式d(P,0)=|x-0|+|y-0|≤2,即|x|+|y|≤2,
对应的图形是以原点为中心,各个顶点在坐标轴上且对角线长为4的正方形及其内部,如图所示
∴所求图形的面积为S=
×42=8;故②正确
对于③到M(0,-2),N(0,2)两点的“折线距离”相等点的集合是{(x,y)||x|+|y+2|=|x|+|y-2|},
即|y+2|=|y-2|,解得y=0,故到M(0,-2),N(0,2)两点的“折线距离”相等的点的轨迹方程是y=0,故③正确
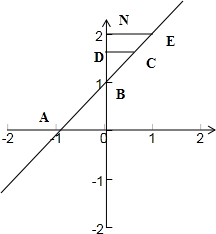
对于④设直线与两轴的交点分别为A(-1,0),B(0,1),设C(x,y)为直线上任意一点,作CD⊥x轴于N,于是有|CD|=|BD|,
所以d=|ND|+|CD|=|ND|+|BD|,
过B作x轴的垂线交直线y=x+1上于点E,
则当C在线段AE上时,d=|ND|+|CD|=|ND|+|BD|=|BN|,
当M在直线y=x+1上且在线段AG外时,d=|ND|+|CD|=|ND|+|BD|>|BN|,
所以,d(N,C)的最小值为|BN|=1,故④正确;
故真命题有:②③④.
故选:C.
对于②根据题意,到坐标原点O的“折线距离”小于等于2的点P(x,y)满足等式d(P,0)=|x-0|+|y-0|≤2,即|x|+|y|≤2,
对应的图形是以原点为中心,各个顶点在坐标轴上且对角线长为4的正方形及其内部,如图所示
∴所求图形的面积为S=
| 1 |
| 2 |

对于③到M(0,-2),N(0,2)两点的“折线距离”相等点的集合是{(x,y)||x|+|y+2|=|x|+|y-2|},
即|y+2|=|y-2|,解得y=0,故到M(0,-2),N(0,2)两点的“折线距离”相等的点的轨迹方程是y=0,故③正确
对于④设直线与两轴的交点分别为A(-1,0),B(0,1),设C(x,y)为直线上任意一点,作CD⊥x轴于N,于是有|CD|=|BD|,
所以d=|ND|+|CD|=|ND|+|BD|,
过B作x轴的垂线交直线y=x+1上于点E,
则当C在线段AE上时,d=|ND|+|CD|=|ND|+|BD|=|BN|,
当M在直线y=x+1上且在线段AG外时,d=|ND|+|CD|=|ND|+|BD|>|BN|,
所以,d(N,C)的最小值为|BN|=1,故④正确;

故真命题有:②③④.
故选:C.
点评:本题主要考查了“折线距离”的定义,以及分析问题解决问题的能力,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
将函数y=sin(x-
)(x∈R)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得到的图象向左平移
个单位长度,则得到的图象的函数单调增区间(其中k∈Z)为( )
| π |
| 3 |
| π |
| 3 |
| A、[4kπ-π,4kπ+π] | ||||
B、[4kπ-
| ||||
C、[kπ-
| ||||
D、[4kπ-
|
已知与正整数n有关的命题P(n)满足:假设P(k)成立,则P(k+1)成立,下列说法一定不存在的是( )
| A、P(2)成立,但P(1)不成立 |
| B、P(1),P(2)均成立 |
| C、P(2)不成立,但P(1)成立 |
| D、P(1),P(2)均不成立 |
已知数列的通项公式an=2n-37,则Sn取最小值时n=( )
| A、18 | B、19 |
| C、18或19 | D、20 |
经过点(0,-2)且在两坐标轴上截距和为2的直线方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
复数z满足z(2+i)=2i-1,则复数z的实部与虚部之和为( )
| A、1 | B、-1 | C、2 | D、3 |
阅读程序框图(如图),执行相应的程序,输出的结果是( )


| A、50 | B、55 |
| C、1023 | D、2565 |
在数列{an}中,a1=1,an+2+(-1)nan=2,记Sn为数列{an}的前项和,则S61=( )
| A、931 | B、961 |
| C、991 | D、1021 |
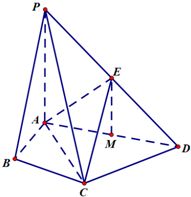 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,M为AD的中点,PA=2AB=4.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,M为AD的中点,PA=2AB=4.