Question

现有构成系统的4个元件，每个元件正常工作的概率均为p(0＜p＜1)，且各个元件能否正常工作是相互独立的，将4个元件按图所示的两种联结方式构成两个系统(1)(2)：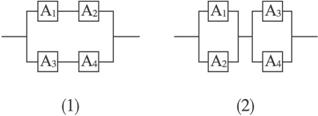

若系统(1)正常工作的概率为p₁,系统(2)正常工作的概率为p₂,则p₁与p₂的大小关系为(    )

A.p₁＞p₂                 B.p₁=p₂            C.p₁＜p₂             D.不确定

Answer 1

答案：C

解析：因A₁，A₂，A₃，A₄相互独立，故系统(1)正常工作的概率p₁=1-［1-P(A₁·A₂)］［1-P(A₃·A₄)］=1-(1-p²)².系统(2)正常工作的概率

p₂=P(A₁+A₂)·P(A₃+A₄)

=［1-P()］·［1-P()］=［1-(1-p)²］².

∴p₁-p₂=1-(1-p²)²-［1-(1-p)²］²

=-2p⁴+4p³-2p²=-2p²(p-1)²＜0,

∴p₁＜p₂.