题目内容
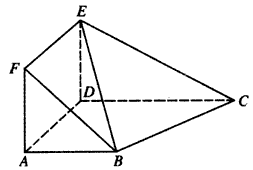
如图所示，正方形ADEF与梯形ABCD所在的平面互相垂直，AD⊥CD，AB∥CD，CD=2AB=2AD．（Ⅰ）求证：BC⊥BE；
（Ⅱ）在EC上找一点M，使得BM∥平面ADEF，请确定M点的位置，并给出证明．
分析：（I）由已知梯形中AD⊥CD，AB∥CD，CD=2AB=2AD，易证BD⊥CB，要证明BC⊥BE，可转化为证BC⊥平面BDE，由已知可得DE⊥平面ABCD从而可得DE⊥BC，由线面垂直的判定定理可得
（II）由已知CD=2AB=2AD．考虑取CD的中点N，BN∥AD，从而有BN∥平面ADEF，当M为EC的中点时，有MN∥DE，则MN∥平面ADEF
（II）由已知CD=2AB=2AD．考虑取CD的中点N，BN∥AD，从而有BN∥平面ADEF，当M为EC的中点时，有MN∥DE，则MN∥平面ADEF
解答：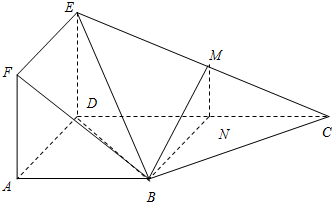
证明：
（Ⅰ）因为正方形ADEF与梯形ABCD所在的平面互相垂直，DE⊥AD
所以DE⊥平面ABCD∴DE⊥BC（1分）
因为AB=AD，所以∠ADB=∠BDC=
，BD=
=
AD
取CD中点N，连接BN
则由题意知：四边形ABND为正方形
所以BC=
=
=
=
AD，BD=BC
则△BDC为等腰直角三角形
则BD⊥BC（5分）
则BC⊥平面BDE
则BC⊥BE（7分）
（Ⅱ）取EC中点M，则有BM∥平面ADEF（8分）
证明如下：连接MN
由（Ⅰ）知BN∥AD，所以BN∥平面ADEF
又因为M、N分别为CE、CD的中点，所以MN∥DE
则MN∥平面ADEF（10分）
则平面BMN∥平面ADEF，所以BM∥平面ADEF（12分）
证明：（Ⅰ）因为正方形ADEF与梯形ABCD所在的平面互相垂直，DE⊥AD
所以DE⊥平面ABCD∴DE⊥BC（1分）
因为AB=AD，所以∠ADB=∠BDC=
| π |
| 4 |
| AD2+AB2 |
| 2 |
取CD中点N，连接BN
则由题意知：四边形ABND为正方形
所以BC=
| BN2+CN2 |
AD2+
|
| AD2+AD2 |
| 2 |
则△BDC为等腰直角三角形
则BD⊥BC（5分）
则BC⊥平面BDE
则BC⊥BE（7分）
（Ⅱ）取EC中点M，则有BM∥平面ADEF（8分）
证明如下：连接MN
由（Ⅰ）知BN∥AD，所以BN∥平面ADEF
又因为M、N分别为CE、CD的中点，所以MN∥DE
则MN∥平面ADEF（10分）
则平面BMN∥平面ADEF，所以BM∥平面ADEF（12分）
点评：本题主要考查了直线平面垂直的判定，直线与平面垂直的性质定理，及“线线垂直、线面垂直、面面垂直的相互转化，还考查了线面平行的判定．
练习册系列答案
阅读快车系列答案
相关题目
（2012•金华模拟）如图所示的正方形中，将边AB、AD各4等分，分别作AB、AD的平行线段成4×4方格网，则从图中取出一由网格线形成的矩形，恰好为正方形的概率是
