题目内容

4．已知命题p：“方程x2+y2-x+y+m=0对应的曲线是圆”，命题q：“函数f（x）=lg（mx2-4x+m）的定义域为R”．若这两个命题中只有一个是真命题，求实数m的取值范围．

分析 求出p，q为真命题时m的范围，分类讨论p真q假时，p假q真时判断，最后求并集．

解答 解：若p真，由（-1）2+12-4m＞0得：$m＜\frac{1}{2}$．…（4分）
若q真，需满足△＜0且m＞0，即$\left\{\begin{array}{l}m＞0\\ 16-4{m^2}＜0\end{array}\right.$，解得m＞2．…（8分）
p真q假时，$m＜\frac{1}{2}$；p假q真时，m＞2．
所以$m∈（-∞，\frac{1}{2}）∪（2，+∞）$．…（12分）

点评 本题考查了命题的真假判断和对命题的分类讨论，属于基础题型，应熟练掌握．

练习册系列答案
相关题目
20．定义在R上的函数f（x）的导函数为f'（x），满足xf'（x）+f（x）＞x，则不等式$（{x-4}）f（{x-4}）-4f（4）＜\frac{x^2}{2}-4x$的解集为（-∞，8）．
15．已知等差数列{an}的公差d≠0，且a1，a3，a13成等比数列，若a1=1，Sn为数列{an}的前n项和，则$\frac{2{S}_{n}+16}{{a}_{n}+3}$的最小值为（　　）
A．4B．3C．2$\sqrt{3}$-2D．2
12．已知圆C：（x-1）2+（y+2）2=5，直线l1：2x-3y+6=0，则与l1平行且过圆C圆心的直线l的方程为2x-3y-8=0．
19．已知具有线性相关的两个变量x，y之间的一组数据如表：
x01234
y24.24.54.6m
且回归方程是y=0.65x+2.7，则m=（　　）
A．5.6B．5.3C．5.0D．4.7
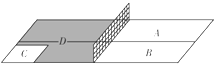9．乓球台面被网分隔成甲、乙两部分，如图，甲上有两个不相交的区域A、B，乙被划分为两个不相交的区域C、D．某次测试要求队员接到落点在甲上的来球后向乙回球．规定：回球一次，落点在C上记3分，在D上记1分，其它情况记0分．对落点在A上的来球，队员小明回球的落点在C上的概率为$\frac{1}{2}$，在D上的概率为$\frac{1}{3}$；对落点在B上的来球，小明回球的落点在C上的概率为$\frac{1}{5}$，在D上的概率为$\frac{3}{5}$．假设共有两次来球且落在A、B上各一次，小明的两次回球互不影响．求：
（1）小明两次回球的落点中恰有一次的落点在乙上的概率；
（2）两次回球结束后，小明得分之和ξ的分布列与均值．
16．若a，b∈R，则复数（a2-6a+10）+（-b2+4b-5）i对应的点在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
13．已知数列{an}的前n项和${S_n}={2^{n+2}}-4{\;}^{\;}（{n∈{N^*}}）$，数列{bn}满足${b_{n+1}}={b_n}+\frac{1}{2}$，b1=1
（1）分别求数列{an}、{bn}的通项公式；
（2）若数列{cn}满足cn=an•bn，Tn是数列{cn}的前n项和，若存在正实数k，使不等式$k（{n^2}-9n+36）{T_n}＞6{n^2}{a_n}$对于一切的n∈N*恒成立，求k的取值范围．
14．命题“?x0∈∁RQ，x02∈Q”的否定是（　　）
A．?x0∈∁RQ，x02∈QB．?x0∈∁RQ，x02∉QC．?x∉∁RQ，x2∈QD．?x∈∁RQ，x2∉Q

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网