题目内容
(本小题满分12分)
已知函数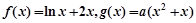 .
.
(1)若 ,求
,求 的单调区间;
的单调区间;
(2)若 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知函数
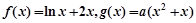 .
.(1)若
 ,求
,求 的单调区间;
的单调区间;(2)若
 恒成立,求
恒成立,求 的取值范围.
的取值范围.(1)增区间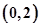 ,减区间
,减区间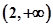 (2)
(2)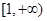
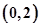 ,减区间
,减区间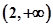 (2)
(2)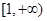
试题分析:(Ⅰ)
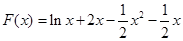 ,其定义域是
,其定义域是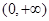 …………1分
…………1分 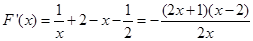
令
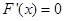 ,得
,得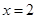 ,
,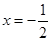 (舍去)。 …………… 3分
(舍去)。 …………… 3分当
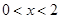 时,
时,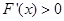 ,函数单调递增;
,函数单调递增;当
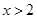 时,
时,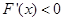 ,函数单调递减;
,函数单调递减;即函数
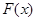 的单调区间为
的单调区间为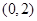 ,
,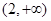 。 ……………… 6分
。 ……………… 6分(Ⅱ)设
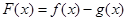 ,则
,则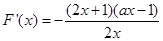 , ………… 7分
, ………… 7分当
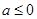 时,
时,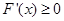 ,
,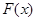 单调递增,
单调递增,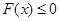 不可能恒成立,
不可能恒成立,当
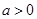 时,令
时,令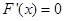 ,得
,得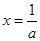 ,
,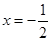 (舍去)。
(舍去)。当
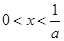 时,
时,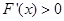 ,函数单调递增; 当
,函数单调递增; 当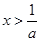 时,
时,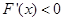 ,函数单调递减;
,函数单调递减; 故
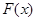 在
在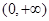 上的最大值是
上的最大值是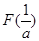 ,依题意
,依题意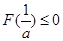 恒成立, …………… 9分
恒成立, …………… 9分即
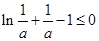 ,…又
,…又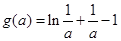 单调递减,且
单调递减,且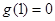 ,………10分
,………10分故
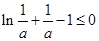 成立的充要条件是
成立的充要条件是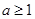 ,所以
,所以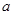 的取值范围是
的取值范围是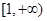 ……… 12分
……… 12分点评:函数
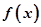 中令
中令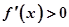 得增区间,令
得增区间,令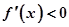 得减区间,第二问中不等式恒成立问题转化为求函数最值问题,在求解过程中用到了函数单调性
得减区间,第二问中不等式恒成立问题转化为求函数最值问题,在求解过程中用到了函数单调性
练习册系列答案
相关题目
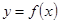 满足:对任意的实数
满足:对任意的实数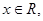 有
有
 的解析式;
的解析式;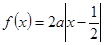 有解,求实数
有解,求实数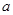 的取值范围.
的取值范围.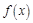 满足
满足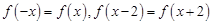 ,且当
,且当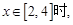
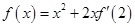 ,则
,则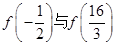 的大小关系是( )
的大小关系是( )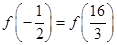 B.
B.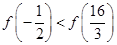 C.
C.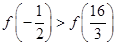 D.不确定
D.不确定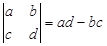 ,函数
,函数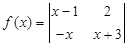 图像的顶点是
图像的顶点是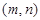 ,且
,且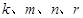 成等差数列,则
成等差数列,则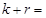 ( )
( )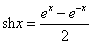 ,
, ”为双曲正弦函数,“
”为双曲正弦函数,“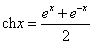 ,
,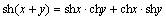 、
、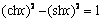 等.请你再写出一个类似的性质:
等.请你再写出一个类似的性质: .
.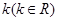 如何取值时,函数
如何取值时,函数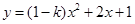 存在零点,并求出零点.
存在零点,并求出零点.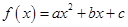 ,且
,且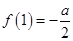 ,
,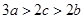 ,求证:(1)
,求证:(1)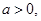 且
且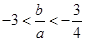 ;
;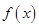 在区间
在区间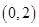 内至少有一个零点;
内至少有一个零点;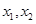 是函数
是函数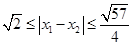 .
.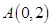 ,
,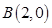 ,若点
,若点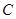 在函数
在函数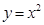 的图象上,则使得
的图象上,则使得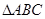 的面积为2的点
的面积为2的点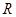 上的函数
上的函数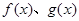 满足
满足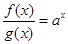 ,且
,且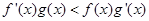 ,
, 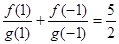 ,若有穷数列
,若有穷数列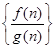 (
(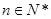 )的前
)的前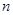 项和等于
项和等于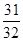 ,则
,则