题目内容
{an}为等差数列，a1+a4+a7=39，a3+a6+a9=27，则S9= ．
考点：等差数列的性质
专题：等差数列与等比数列
分析：两式相加结合等差数列的性质可得a5=5，而S9=9a5，代入可得．
解答：
解：在等差数列{an}中，由a1+a4+a7=39，a3+a6+a9=27，
两式相加可得a1+a4+a7+a3+a6+a9=39+27=66，
而由等差数列的性质可得a1+a9=a4+a6=a7+a3=2a5，
故可得6a5=66，解得a5=11，
故S9=
=9a5=99，
故答案为：99．
两式相加可得a1+a4+a7+a3+a6+a9=39+27=66，
而由等差数列的性质可得a1+a9=a4+a6=a7+a3=2a5，
故可得6a5=66，解得a5=11，
故S9=
| 9(a1+a9) |
| 2 |
故答案为：99．
点评：本题考查等差数列的性质和求和公式，属基础题．
练习册系列答案
全能练考卷系列答案
相关题目
复数1-i在复平面内对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
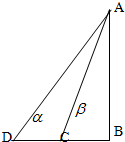如图：D，C，B三点在地面同一直线上，DC=a，从C，D两点测得A点仰角分别是β，α（α＜β），则A点离地面的高度AB等于