题目内容
函数f（x）的定义域为D，若对于任意x1，x2∈D，当x1＜x2时，都有f（x1）≤f（x2），则称函数f（x）在D上为非减函数．设函数f（x）为定义在[0，1]上的非减函数，且满足以下三个条件：
①f（0）=0；②f（1﹣x）+f（x）=1x∈[0，1]； ③当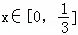
时，
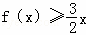恒成立．则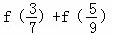
= ．
解：∵函数f（x）满足：f（1﹣x）+f（x）=1，x∈[0，1]，则f（
）=，且当
时，
恒成立，
则f（
）≥
，又∵函数f（x）为定义在[0，1]上的非减函数，∴当x∈[
，]时，f（x）=，恒成立，故f（
）=，f（
）=，则f（
）=
，则
=1故答案为1．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
，
，
，则数列
成 （ ） 
的公差
，且
成等比数列，则
（ ）
B、
C、
D、
（Ⅰ）求函数
的定义域；
满足
，试求实数
的取值范围.
，集合
.若
中恰含有一个整数，则实数
的取值范围是（ ）A．
B．
C．
D．
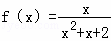．其中属于有界泛函的是（ ）
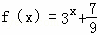，则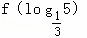
的值等于 ．
，若数列
满足
，且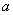
的取值范围是（ 
）
. 
B. 
C. 
D. 
是定义域为R的偶函数，且
, 
。