题目内容
设函数f(x)的定义域为R,若存在与x无关的正常数M,使|f(x)|≤M|x|对一切实数x恒成立,则称f(x)为有界泛函.有下面四个函数:
①f(x)=1; ②f(x)=x2; ③f(x)=2xsinx; ④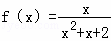 .其中属于有界泛函的是( )
.其中属于有界泛函的是( )
|
| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
B解:对于①,显然不存在M都有1≤M|x|成立,故①错;对于②,|f(x)|=|x2|≤M|x|,即|x|≤M,不存在这样的M对一切实数x均成立,故不是有界泛函;②错对于③,f(x)|=|2xsinx|≤M|x|,即|2sinx|≤M,当M≥2时,f(x)=3xsinx是有界泛函..③对对于④,| |)|≤M|x|,即
|)|≤M|x|,即 ≤M,只需
≤M,只需 ,④对综上所述,③④故选B
,④对综上所述,③④故选B

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 上的函数
上的函数 满足:
满足:
 设数列
设数列 的前
的前 项和为
项和为 ,则
,则 B.
B.  C.
C.  D.
D.
 的值域为
的值域为 ) B.(—
) B.(— ] C.(0,
] C.(0,




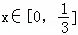 时,
时,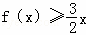 恒成立.则
恒成立.则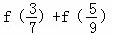 = .
= . ,则对任意
,则对任意 ,若
,若 ,下列不等式成立的是
,下列不等式成立的是 B.
B.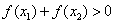
 D.
D.
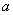 是函数
是函数 的零点,若
的零点,若 的值满足( )
的值满足( ) B.
B. C.
C. D.
D. 的符号不能确定
的符号不能确定  )=n.
)=n.