题目内容
已知偶函数y=f(x)满足条件f(x+1)=f(x﹣1),且当x∈[﹣1,0]时,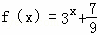 ,则
,则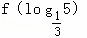 的值等于 .
的值等于 .

解:由f(x+1)=f(x﹣1),得f(x+2)=f(x),所以f(x)是以2为周期的周期函数,又f(x)为偶函数,
所以 =f(log35)=f(log35﹣2)=f(
=f(log35)=f(log35﹣2)=f( )=
)= +
+ =
= =
= ,故答案为:.
,故答案为:.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
若数列{an}满足:存在正整数T,对于任意正整数n都有an+T=an成立,则称数列{an}为周期数列,周期为T.已知数列{an}满足a1=m(m>0),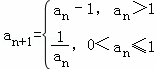 则下列结论中错误的是( )
则下列结论中错误的是( )
|
| A. | 若a3=4,则m可以取3个不同的值 |
|
| B. | 若 |
|
| C. | ∀T∈N*且T≥2,存在m>1,使得{an}是周期为T的数列 |
|
| D. | ∃m∈Q且m≥2,使得数列{an}是周期数列 |
 ,则数列{an}是周期为3的数列
,则数列{an}是周期为3的数列 ,x∈
,x∈ ,则满足f(x0)>f(
,则满足f(x0)>f( )的x0的取值范围为 .
)的x0的取值范围为 .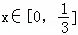 时,
时,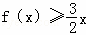 恒成立.则
恒成立.则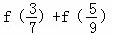 = .
= .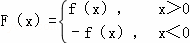 给出下列命题:
给出下列命题: ,则对任意
,则对任意 ,若
,若 ,下列不等式成立的是
,下列不等式成立的是 B.
B.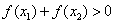
 D.
D.
 ,若
,若 在
在 上恒成立,则实数
上恒成立,则实数 的取值范围( )
的取值范围( ) (B)
(B) (C)
(C) (D)
(D)

 是偶函数,则
是偶函数,则 的值为
的值为 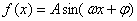 (其中A>0,|ω|<
(其中A>0,|ω|< )的图象如图所示,为得到
)的图象如图所示,为得到 的图象,则只要将
的图象,则只要将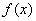 的图象( )A. 向右平移
的图象( )A. 向右平移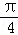 个单位长度 B. 向右平移
个单位长度 B. 向右平移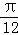 个单位长度
个单位长度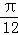 个单位长度
个单位长度