题目内容
【题目】已知函数![]() 有两个零点.
有两个零点.
(1)求实数![]() 的取值范围;
的取值范围;
(2)设![]() ,
, ![]() (
(![]() )是
)是![]() 的两个零点,证明:
的两个零点,证明: ![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】【试题分析】(1)先对函数求导,然后对![]() 分成
分成![]() 两类,结合函数两个零点,研究函数的单调区间,由此求得
两类,结合函数两个零点,研究函数的单调区间,由此求得![]() 的取值范围.(2)将要证明的不等式,利用函数
的取值范围.(2)将要证明的不等式,利用函数![]() ,等价转化为证明
,等价转化为证明![]() ,构造函数令
,构造函数令![]() ,利用导数求得
,利用导数求得![]() 由此证得不等式成立.
由此证得不等式成立.
【试题解析】
解:(1)∵![]() ,
, ![]() .
.
(2)当![]() 时,
时, ![]() 在
在![]() 上恒成立,∴
上恒成立,∴![]() 在
在![]() 上单调递增,显然不符合题意.
上单调递增,显然不符合题意.
(3)当![]() 时,由
时,由![]() ,得
,得![]() ,
,
|
|
|
|
|
|
|
|
| 递减 | 极小值 | 递增 |
当![]() →
→![]() ,
, ![]() →
→![]() 时都有
时都有![]() →
→![]() ,
,
当![]() ,即
,即![]() 时
时![]() 有两个零点.
有两个零点.
(2)要证![]() ,即证
,即证![]() ,
,
由已知![]() ,
, ![]() ,
,
即证![]() ,
,
即证![]() ,即证
,即证![]() ,即证
,即证![]() ,
,
又∵![]() ,且
,且![]() 在
在![]() 单调递增,
单调递增,
故只需证![]() ,即证
,即证![]() ,
,
令![]() 且
且![]() ,
,
∵![]()
![]()
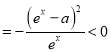 ,
,
∴![]() 在
在![]() 单调递减,∴
单调递减,∴![]() ,
,
∴![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() ,故原命题得证.
,故原命题得证.

练习册系列答案
相关题目
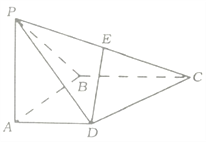
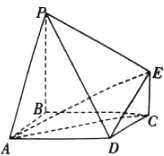
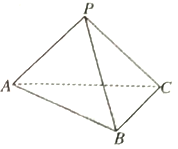
【题目】在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点,
的中点, ![]() 是线段
是线段![]() 上一个动点,且
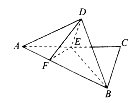
上一个动点,且![]() ,如图所示,沿
,如图所示,沿![]() 将
将![]() 翻折至
翻折至![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.
(1)当![]() 时,证明:
时,证明: ![]() 平面
平面![]() ;
;
(2)是否存在![]() ,使得三棱锥
,使得三棱锥![]() 的体积是
的体积是![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【题目】某地![]() 户家庭的年收入
户家庭的年收入![]() (万元)和年饮食支出
(万元)和年饮食支出![]() (万元)的统计资料如下表:
(万元)的统计资料如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程;(结果保留到小数点后
的线性回归方程;(结果保留到小数点后![]() 为数字)
为数字)
(2)利用(1)中的回归方程,分析这![]() 户家庭的年饮食支出的变化情况,并预测该地年收入
户家庭的年饮食支出的变化情况,并预测该地年收入![]() 万元的家庭的年饮食支出.(结果保留到小数点后
万元的家庭的年饮食支出.(结果保留到小数点后![]() 位数字)
位数字)
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
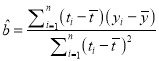 ,
, ![]()