题目内容
如图,已知双曲线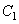 :
: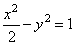 ,曲线
,曲线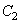 :
: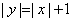 .
.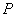 是平面内一点,若存在过点
是平面内一点,若存在过点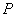 的直线与
的直线与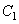 、
、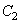 都有公共点,则称
都有公共点,则称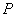 为“
为“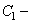
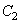 型点”.
型点”.
(1)在正确证明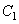 的左焦点是“
的左焦点是“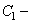
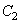 型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线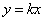 与
与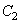 有公共点,求证
有公共点,求证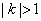 ,进而证明原点不是“
,进而证明原点不是“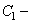
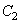 型点;
型点;
(3)求证:圆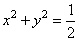 内的点都不是“
内的点都不是“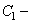
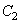 型点”.
型点”.
 |
解:(1)C1的左焦点为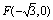 ,过F的直线
,过F的直线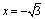 与C1交于
与C1交于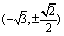 ,
,
与C2交于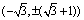 ,故C1的左焦点为“C1-C2型点”,且直线可以为
,故C1的左焦点为“C1-C2型点”,且直线可以为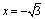 ;
;
(2)直线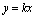 与C2有交点,则
与C2有交点,则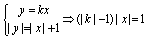 ,若方程组有解,则必须
,若方程组有解,则必须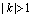 ;
;
直线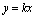 与C2有交点,则
与C2有交点,则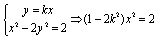 ,若方程组有解,则必须
,若方程组有解,则必须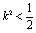
故直线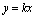 至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”。
至多与曲线C1和C2中的一条有交点,即原点不是“C1-C2型点”。
(3)显然过圆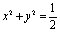 内一点的直线
内一点的直线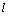 若与曲线C1有交点,则斜率必存在;
若与曲线C1有交点,则斜率必存在;
根据对称性,不妨设直线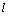 斜率存在且与曲线C2交于点
斜率存在且与曲线C2交于点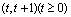 ,则
,则
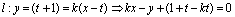 ,直线
,直线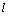 与圆
与圆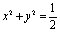 内部有交点,故
内部有交点,故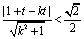
化简得,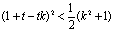 。。。。。。。。。。。。①
。。。。。。。。。。。。①
若直线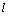 与曲线C1有交点,则
与曲线C1有交点,则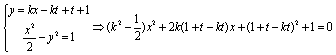
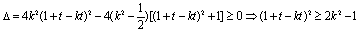 ,化简得,
,化简得,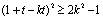 。。。②
。。。②
由①②得,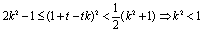
但此时,因为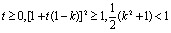 ,即①式不成立;当
,即①式不成立;当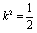 时,①式也不成立
时,①式也不成立
综上,直线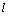 若与圆
若与圆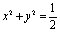 内有交点,则不可能同时与曲线C1和C2有交点,即圆
内有交点,则不可能同时与曲线C1和C2有交点,即圆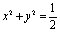 内的点都不是“C1-C2型点” .
内的点都不是“C1-C2型点” .

练习册系列答案
相关题目
 在
在 上是单调减函数,则实数
上是单调减函数,则实数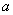 的取值范围是
的取值范围是 ,则n的取值范围为( )
,则n的取值范围为( )
 ,则直线
,则直线 的倾斜角的取值范围是 。
的倾斜角的取值范围是 。 与双曲线
与双曲线 的渐近线交于
的渐近线交于 两点,设
两点,设 为双曲线
为双曲线 上的任意一点,若
上的任意一点,若 (
( ,
, 为坐标原点),则下列不等式恒成立的是 ( )
为坐标原点),则下列不等式恒成立的是 ( ) (B)
(B) (C)
(C) (D)
(D)
 ,
, ,则
,则 =( )
=( ) B.
B. C.
C. D.
D.
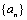 中,若公比
中,若公比 ,且前3项之和等于21,则该数列的通项公式
,且前3项之和等于21,则该数列的通项公式 .
. ,若点
,若点 为平面区域
为平面区域 上的一个动点,则|AM|的最小值是
上的一个动点,则|AM|的最小值是 B.
B. C.
C. D.
D.
 上,且点P到x轴的距离与点P到此抛物线的焦点的距离之比为
上,且点P到x轴的距离与点P到此抛物线的焦点的距离之比为 ,则点P到x轴的距离是
,则点P到x轴的距离是 (B)
(B) (C)1 (D)2
(C)1 (D)2