题目内容
在△ABC中，a，b，c分别为角A，B，C所对边，若sinA=2sinBsinC，则此三角形一定是（ ）
| A、等腰直角三角形 |
| B、等腰或直角三角形 |
| C、等腰三角形 |
| D、直角三角形 |
考点：正弦定理
专题：解三角形
分析：由于sinA=2sinBsinC，A=π-（B+C），可得sin（B+C）=2sinBsinC，展开化为sin（B-C）=0，由于（B-C）∈（-π，π）．即可得出．
解答：
解：∵sinA=2sinBsinC，A=π-（B+C），
∴sin（B+C）=2sinBsinC，
化为sin（B-C）=0，
∵（B-C）∈（-π，π）．
∴B=C．
∴此三角形一定是等腰三角形．
故选：C．
∴sin（B+C）=2sinBsinC，
化为sin（B-C）=0，
∵（B-C）∈（-π，π）．
∴B=C．
∴此三角形一定是等腰三角形．
故选：C．
点评：本题考查了解三角形的方法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
sin42°cos18°+cos42°sin18°=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
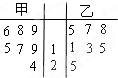某赛季，甲、乙两名篮球运动员都参加了7场比赛，他们所有比赛得分的情况用如图所示的茎叶图表示，则甲运动员得分的中位数，乙运动员的平均数分别为（ ）| A、15、12 |
| B、15、15 |
| C、19、11 |
| D、19、15 |