题目内容
 如图,在四边形ABCD中,已知AB=13,AC=10,AD=5,CD=
如图,在四边形ABCD中,已知AB=13,AC=10,AD=5,CD= ,
,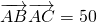
(1)求cos∠BAC的值;
(2)求sin∠CAD的值;
(3)求△BAD的面积.
解:(1)在四边形ABCD中,已知AB=13,AC=10,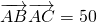 ,则有 cos∠BAC=
,则有 cos∠BAC= =
= =
= .
.
(2)在△ADC中,AC=10,AD=5,CD= ,cos∠CAD=
,cos∠CAD= =
= ,∴sin∠CAD=
,∴sin∠CAD= .
.
(3)由(1)可得cos∠BAC= ,∴sin∠BAC=
,∴sin∠BAC= ,从而sin∠BAD=sin(∠BAC+∠CAD)=sin∠BAC•cos∠CAD+cos∠BAC•sin∠CAD
,从而sin∠BAD=sin(∠BAC+∠CAD)=sin∠BAC•cos∠CAD+cos∠BAC•sin∠CAD
=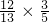 +
+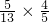 =
= ,
,
∴△BAD的面积S= =28.
=28.
分析:(1)在四边形ABCD中,根据cos∠BAC= 运算求得结果.
运算求得结果.
(3)根据cos∠BAC= ,求得sin∠BAC=
,求得sin∠BAC= ,从而利用两角和的正弦公式求得sin∠BAD=sin(∠BAC+∠CAD) 的值,再由△BAD的面积S=
,从而利用两角和的正弦公式求得sin∠BAD=sin(∠BAC+∠CAD) 的值,再由△BAD的面积S= 求得结果.
求得结果.
点评:本题主要考查余弦定理的应用,两个向量夹角公式、两角和的正弦公式的应用,属于中档题.
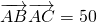 ,则有 cos∠BAC=
,则有 cos∠BAC= =
= =
= .
.(2)在△ADC中,AC=10,AD=5,CD=
 ,cos∠CAD=
,cos∠CAD= =
= ,∴sin∠CAD=
,∴sin∠CAD= .
.(3)由(1)可得cos∠BAC=
 ,∴sin∠BAC=
,∴sin∠BAC= ,从而sin∠BAD=sin(∠BAC+∠CAD)=sin∠BAC•cos∠CAD+cos∠BAC•sin∠CAD
,从而sin∠BAD=sin(∠BAC+∠CAD)=sin∠BAC•cos∠CAD+cos∠BAC•sin∠CAD =
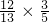 +
+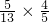 =
= ,
,∴△BAD的面积S=
 =28.
=28.分析:(1)在四边形ABCD中,根据cos∠BAC=
 运算求得结果.
运算求得结果.(3)根据cos∠BAC=
 ,求得sin∠BAC=
,求得sin∠BAC= ,从而利用两角和的正弦公式求得sin∠BAD=sin(∠BAC+∠CAD) 的值,再由△BAD的面积S=
,从而利用两角和的正弦公式求得sin∠BAD=sin(∠BAC+∠CAD) 的值,再由△BAD的面积S= 求得结果.
求得结果.点评:本题主要考查余弦定理的应用,两个向量夹角公式、两角和的正弦公式的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在四边形ABCD中,△ABC为边长等于
如图,在四边形ABCD中,△ABC为边长等于 如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=7,AD=6,S△ADC=
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=7,AD=6,S△ADC= 如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=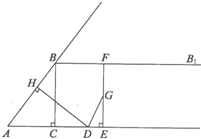 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒. (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,