题目内容
(本小题满分14分)已知椭圆C: 的右焦点为F,右顶点为A,离心率为e,点
的右焦点为F,右顶点为A,离心率为e,点 满足条件
满足条件 .
.
(Ⅰ)求m的值;
(Ⅱ)设过点F的直线l与椭圆C相交于M,N两点,记 和
和 的面积分别为
的面积分别为 ,
, ,若
,若 ,求直线l的方程.
,求直线l的方程.
(Ⅰ) ; (Ⅱ)直线l的方程为
; (Ⅱ)直线l的方程为  或
或  .
.
【解析】
试题分析:(Ⅰ)【解析】
因为椭圆C的方程为  ,根据椭圆的性质和数据建立方程即可求出结果;
,根据椭圆的性质和数据建立方程即可求出结果;
(Ⅱ)若直线l的斜率不存在,则有  ,不合题意. 若直线l的斜率存在,设直线l的方程为
,不合题意. 若直线l的斜率存在,设直线l的方程为 ,
,
由  得
得  ,利用韦达定理和题中所给关系即可求出直线的斜率,进而求出直线的方程.
,利用韦达定理和题中所给关系即可求出直线的斜率,进而求出直线的方程.
试题解析:(Ⅰ)【解析】
因为椭圆C的方程为  ,
,
所以  ,
, ,
, , 2分
, 2分
则  ,
, ,
, . 3分
. 3分
因为  ,
,
所以  . 5分
. 5分
(Ⅱ)【解析】
若直线l的斜率不存在,则有  ,不合题意. 6分
,不合题意. 6分
若直线l的斜率存在,设直线l的方程为 ,
, ,
, .
.
由 
得  , 7分
, 7分
可知  恒成立,且
恒成立,且  ,
, . 8分
. 8分
因为 和
和 的面积分别为
的面积分别为 ,
, ,
,
所以 . 9分
. 9分
即  .
.
所以  ,
, , 11分
, 11分
则  ,
,
即  ,
,
即  ,
,
解得  . 13分
. 13分
所以直线l的方程为  或
或  . 14分
. 14分
考点:1.椭圆的性质;2.直线与椭圆的位置关系.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 ,则
,则  中元素的个数为_______.
中元素的个数为_______. (
( ),若
),若 ,则实数
,则实数 的值为__________.
的值为__________.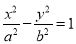 的虚轴长为2,焦距为
的虚轴长为2,焦距为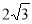 ,则此双曲线的离心率为( ).
,则此双曲线的离心率为( ).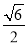 B.
B.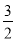 C.
C.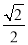 D.
D.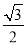

 ,那么实数
,那么实数 ___;
___;  有且仅有两个零点,那么实数
有且仅有两个零点,那么实数 的取值范围是___.
的取值范围是___. 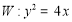 的焦点为F,过F的直线与W相交于A,B两点,记点F到直线l:
的焦点为F,过F的直线与W相交于A,B两点,记点F到直线l: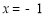 的距离为
的距离为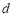 ,则有( )
,则有( )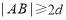 (B)
(B) (C)
(C)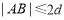 (D)
(D)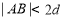
 为双曲线C:
为双曲线C: 的左、右焦点,点P为双曲线C上一点,如果
的左、右焦点,点P为双曲线C上一点,如果 ,那么双曲线C的方程为____;离心率为____.
,那么双曲线C的方程为____;离心率为____.