题目内容
如图所示四边形ABCD内接于E、O，AC交BD于点E，圆的切线DF交BC的延长线于F，CD平分∠BDF（Ⅰ）求证：AB•AD=AC•AE
（Ⅱ）若圆的半径为2，弦BD长为2
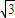，求切线DF的长．
【答案】分析：（Ⅰ）证明△CDA∽△BEA，可得
，从而可得结论；
（Ⅱ）连接OD，OB，利用OD=OB=2，BD=2
，可得∠BCD=120°，从而可得∠BFD=90°，即可求切线DF的长．
解答：（Ⅰ）证明：由弦切角定理可知∠CDF=∠CAD
∵∠CDB=∠CAB，∠FDC=∠BDC
∴∠CAD=∠EAB
∵∠ACD=∠ABD
∴△CDA∽△BEA
∴
∴AB•AD=AC•AE；
（Ⅱ）解：连接OD，OB
在△BOD中，OD=OB=2，BD=2
，
∴∠BCD=120°
∴∠CBD=∠BDC=∠CDF=30°
∴∠BFD=90°
在直角△BFD中，DF=
=
∴切线DF的长为
．
点评：本题考查三角形相似的判定，考查弦切角定理，考查学生的计算能力，属于中档题．
，从而可得结论；（Ⅱ）连接OD，OB，利用OD=OB=2，BD=2
，可得∠BCD=120°，从而可得∠BFD=90°，即可求切线DF的长．解答：（Ⅰ）证明：由弦切角定理可知∠CDF=∠CAD
∵∠CDB=∠CAB，∠FDC=∠BDC
∴∠CAD=∠EAB
∵∠ACD=∠ABD
∴△CDA∽△BEA
∴
∴AB•AD=AC•AE；
（Ⅱ）解：连接OD，OB
在△BOD中，OD=OB=2，BD=2
，∴∠BCD=120°
∴∠CBD=∠BDC=∠CDF=30°
∴∠BFD=90°
在直角△BFD中，DF=
=∴切线DF的长为
．点评：本题考查三角形相似的判定，考查弦切角定理，考查学生的计算能力，属于中档题．
练习册系列答案
华东师大版一课一练系列答案
相关题目
如图所示，四边形PCBM是直角梯形，∠PCB=90°，PM∥BC，PM=PC=AC=1，BC=2，∠ACB=120°，AB⊥PC．
（2012•宝鸡模拟）在如图所示的几何体中，四边形ACC1A1是矩形，FC1∥BC，EF∥A1C1，∠BCC1=90°，点A、B、E、A1在一个平面内，AB=BC=CC1=2，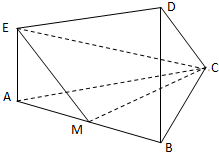
（2012•临沂一模）在如图所示的几何体中，四边形ABDE为梯形，AE∥BD，AE⊥平面ABC，AC⊥BC，AC=BC=BD=2AE，M为AB的中点；
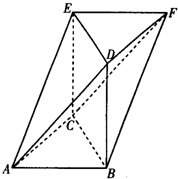如图所示的几何体ABCDFE中，△ABC，△DFE都是等边三角形，且所在平面平行，四边形BCED为正方形，且所在平面垂直于平面ABC．
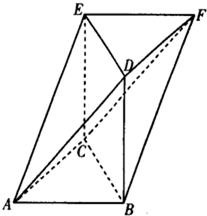如图所示的几何体ABCDFE中，△ABC，△DFE都是等边三角形，且所在平面平行，四边形BCED是边长为2的正方形，且所在平面垂直于平面ABC．