题目内容
 (2012•宝鸡模拟)在如图所示的几何体中,四边形ACC1A1是矩形,FC1∥BC,EF∥A1C1,∠BCC1=90°,点A、B、E、A1在一个平面内,AB=BC=CC1=2,AC=2
(2012•宝鸡模拟)在如图所示的几何体中,四边形ACC1A1是矩形,FC1∥BC,EF∥A1C1,∠BCC1=90°,点A、B、E、A1在一个平面内,AB=BC=CC1=2,AC=2| 2 |
(1)证明:A1E∥AB;
(2)若A1E=C1F=1,求平面BEF与平面ABC所成夹角的正切值.
分析:(1)由已知,可得A1C1∥平面ABC,FC1∥平面ABC,可由面面平行的判定定理可得平面A1EFC1∥平面ABC,进而由面面平行的性质定理可得A1E∥AB;
(2)建立空间直角坐标系,分别求出平面BEF与平面ABC的法向量,利用向量法求出两面角的余弦值,进而根据同角三角函数关系求出答案.
(2)建立空间直角坐标系,分别求出平面BEF与平面ABC的法向量,利用向量法求出两面角的余弦值,进而根据同角三角函数关系求出答案.
解答:证明:(1)∵四边形ACC1A1是矩形,
∴AC∥A1C1,AC?平面ABC
∴A1C1∥平面ABC
∵FC1∥BC,BC?平面ABC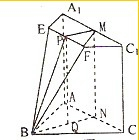
∴FC1∥平面ABC
∵A1C1,FC1?平面A1EFC1,且A1C1∩FC1=C1,
∴平面A1EFC1∥平面ABC
又∵平面ABEA1现平面A1EFC1,平面ABC交线分别为平面A1E、AB
∴A1E∥AB;…6分
解:(2)∵四边形ACC1A1是矩形,
∴AA1∥CC1,
又∵∠BCC1=90°,即CC1⊥BC1,
∴AA1⊥BC
∵AB=BC=2,AC=2
∴AB2+BC2=AC2,
∴∠ABC=90°,即BC⊥AB
又∵AB、AA1?平面ABEA1,
∴BC⊥平面ABEA1,而BC?平面CC1FB
∴平面CC1FB⊥平面ABEA1,
∵AA1⊥AC,AA1⊥BC
∴AA1⊥平面ABC,CC1⊥平面ABC…8分
如图建立空间直角坐标系,
则
=(0,0,2)为平面ABC的一个法向量,…9分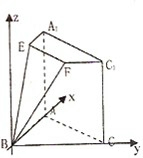
设平面BEF的法向量
=(x,y,z)
∵A1E=C1F=1,
∴E(1,0,2),F(0,1,2)
∴
=(1,0,2),
=(0,1,2)
则
,即
令x=2,则
=(2,2,-1)即为平面BEF的法向量…10分
设平面BEF与平面ABC所成夹角为θ
则cosθ=
=
…11分
则sinθ=
,tanθ=2
…12分
∴AC∥A1C1,AC?平面ABC
∴A1C1∥平面ABC
∵FC1∥BC,BC?平面ABC

∴FC1∥平面ABC
∵A1C1,FC1?平面A1EFC1,且A1C1∩FC1=C1,
∴平面A1EFC1∥平面ABC
又∵平面ABEA1现平面A1EFC1,平面ABC交线分别为平面A1E、AB
∴A1E∥AB;…6分
解:(2)∵四边形ACC1A1是矩形,
∴AA1∥CC1,
又∵∠BCC1=90°,即CC1⊥BC1,
∴AA1⊥BC
∵AB=BC=2,AC=2
| 2 |
∴AB2+BC2=AC2,
∴∠ABC=90°,即BC⊥AB
又∵AB、AA1?平面ABEA1,
∴BC⊥平面ABEA1,而BC?平面CC1FB
∴平面CC1FB⊥平面ABEA1,
∵AA1⊥AC,AA1⊥BC
∴AA1⊥平面ABC,CC1⊥平面ABC…8分
如图建立空间直角坐标系,
则
| CC1 |

设平面BEF的法向量
| n |
∵A1E=C1F=1,
∴E(1,0,2),F(0,1,2)
∴
| BE |
| BF |
则
|
|
令x=2,则
| n |
设平面BEF与平面ABC所成夹角为θ
则cosθ=
|
| ||||
|
|
| 1 |
| 3 |
则sinθ=
2
| ||
| 3 |
| 2 |
点评:本题考查的知识点是空间中直线与直线之间的位置关系,平面与平面平等的判定及性质,向量法求二面角,其中(1)中关键是熟练掌握面面平行,线面平面与线线平行之间的相互转化,(2)的关键是建立空间坐标系,将问题转化为空间向量问题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 (2012•宝鸡模拟)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
(2012•宝鸡模拟)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<