题目内容
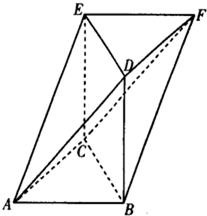如图所示的几何体ABCDFE中，△ABC，△DFE都是等边三角形，且所在平面平行，四边形BCED是边长为2的正方形，且所在平面垂直于平面ABC．（Ⅰ）求几何体ABCDFE的体积；
（Ⅱ）证明：平面ADE∥平面BCF．
分析：（Ⅰ）取BC的中点O，ED的中点G，由条件证明AO⊥平面BCED，同理FG⊥平面BCED，故所求的几何体的体积等于三棱锥F-BCED的体积的2倍，运算求得结果．
（Ⅱ）先证明AO和FG平行且相等，可得四边形AOFG为平行四边形，可得AG∥OF，再证DE∥BC，利用平面和平面平行的判定定理，证得平面ADE∥平面BCF．
（Ⅱ）先证明AO和FG平行且相等，可得四边形AOFG为平行四边形，可得AG∥OF，再证DE∥BC，利用平面和平面平行的判定定理，证得平面ADE∥平面BCF．
解答：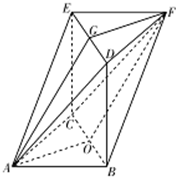
解：（Ⅰ）取BC的中点O，ED的中点G，连接AO，OF，FG，AG．
因为△ABC，△DFE都是等边三角形，故有AO⊥BC，且平面BCED⊥平面ABC，
所以AO⊥平面BCED，同理FG⊥平面BCED，
因为AO=FG=
，四边形BCED是边长为2的正方形，
所以，VABCDFE= 2•V F-BCED=
×4×
×2=
．…（6分）
（Ⅱ）由（Ⅰ）知AO∥FG，AO=FG，
所以四边形AOFG为平行四边形，故AG∥OF，
又DE∥BC，所以，平面ADE∥平面BCF．…（12分）
解：（Ⅰ）取BC的中点O，ED的中点G，连接AO，OF，FG，AG．因为△ABC，△DFE都是等边三角形，故有AO⊥BC，且平面BCED⊥平面ABC，
所以AO⊥平面BCED，同理FG⊥平面BCED，
因为AO=FG=
| 3 |
所以，VABCDFE= 2•V F-BCED=
| 1 |
| 3 |
| 3 |
8
| ||
| 3 |
（Ⅱ）由（Ⅰ）知AO∥FG，AO=FG，
所以四边形AOFG为平行四边形，故AG∥OF，
又DE∥BC，所以，平面ADE∥平面BCF．…（12分）
点评：本题主要考查平面和平面平行的判定定理的应用，用分割法求柱体、椎体的体积，属于中档题．
练习册系列答案
新思维寒假作业系列答案
相关题目
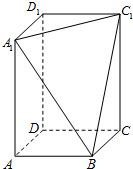在长方体ABCD-A1B1C1D1中，AB=BC=2，过A1、C1、B三点的平面截去长方体的一个角后，得到如图所示的几何体ABCD-A1C1D1，且这个几何体的体积为10．
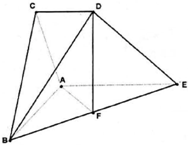如图所示的几何体中，△ABC为正三角形，AE和CD都垂直于平面ABC，且AE=AB=2，CD=1，F为BE的中点．
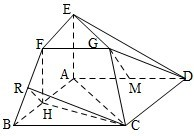在如图所示的几何体中，四边形ABCD为平行四边形，∠ACB=90°，EA⊥平面ABCD，EF∥AB，FG∥BC，EG∥AC．AB=2EF．
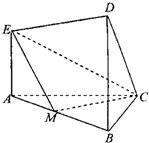在如图所示的几何体中．EA⊥平面ABC，DB⊥平面ABC，AC⊥BC，且AC=BC=BD=2AE=2，M是AB的中点．
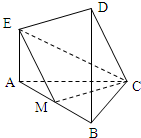在如图所示的几何体中，EA⊥平面ABC，DB⊥平面ABC，AC⊥BC，AC=BC=BD=2AE=2，M是AB的中点．