题目内容
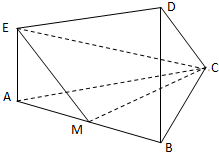 (2012•临沂一模)在如图所示的几何体中,四边形ABDE为梯形,AE∥BD,AE⊥平面ABC,AC⊥BC,AC=BC=BD=2AE,M为AB的中点;
(2012•临沂一模)在如图所示的几何体中,四边形ABDE为梯形,AE∥BD,AE⊥平面ABC,AC⊥BC,AC=BC=BD=2AE,M为AB的中点;(1)求证:CM⊥DE;
(2)求锐二面角D-EC-M的余弦值.
分析:(1)证明CM⊥DE,只需证明CM⊥平面ABDE,利用AE⊥CM,CM⊥AB即可证明;
(2)过M作MO⊥AC,则MO⊥平面AEDC,作MF⊥EC,连接OF,则OF⊥EC,故∠MFO为锐二面角D-EC-M的平面角,从而可求.
(2)过M作MO⊥AC,则MO⊥平面AEDC,作MF⊥EC,连接OF,则OF⊥EC,故∠MFO为锐二面角D-EC-M的平面角,从而可求.
解答:(1)证明:∵AE⊥平面ABC,CM?平面ABC,
∴AE⊥CM
∵AC=BC,M为AB的中点
∴CM⊥AB,又AB∩AE=A
∴CM⊥平面ABDE
∵DE?平面ABDE
∴CM⊥DE;
(2)解:∵AE⊥平面ABC,AE?平面AEDC
∴平面AEDC⊥平面ABC
过M作MO⊥AC,则MO⊥平面AEDC
作MF⊥EC,连接OF,则OF⊥EC,
∴∠MFO为锐二面角D-EC-M的平面角
设AC=BC=BD=2AE=2a,则AM=MC=
a,∴MO=a
△EMC中,EM=
a,MC=
a,EC=
a,
∴△EMC是直角三角形,
∴MF=
=
a
∴cos∠MFO=
=
∴AE⊥CM
∵AC=BC,M为AB的中点
∴CM⊥AB,又AB∩AE=A
∴CM⊥平面ABDE
∵DE?平面ABDE
∴CM⊥DE;
(2)解:∵AE⊥平面ABC,AE?平面AEDC

∴平面AEDC⊥平面ABC
过M作MO⊥AC,则MO⊥平面AEDC
作MF⊥EC,连接OF,则OF⊥EC,
∴∠MFO为锐二面角D-EC-M的平面角
设AC=BC=BD=2AE=2a,则AM=MC=
| 2 |
△EMC中,EM=
| 3 |
| 2 |
| 5 |
∴△EMC是直角三角形,
∴MF=
| EM×MC |
| EC |
| ||
| 5 |
∴cos∠MFO=
| a | ||||
|
| ||
| 6 |
点评:本题考查线面垂直,考查面面角,解题的关键是掌握线面垂直的判定与性质,正确作出面面角.

练习册系列答案
相关题目