利用导数定义求y=$\frac{1}{x}$的导数.并求y′|x=1．题目和参考答案——青夏教育精英家教网——

题目内容

16．利用导数定义求y=$\frac{1}{x}$的导数，并求y′|_x=1．

分析利用定义计算函数变化率的极限即可．

解答解：当x=1时，y=1；当x=1+△x时，y=$\frac{1}{1+△x}$，
∴$\frac{\frac{1}{1+△x}-1}{△x}$=-$\frac{1}{1+△x}$．
∴y′|_x=1=$\underset{lim}{△x→0}$-$\frac{1}{1+△x}$=-1．

点评本题考查了导数的定义，属于基础题．

练习册系列答案

伴你学习新课程单元过关练习系列答案

中考综合学习评价与检测系列答案

新课程初中学习能力自测丛书系列答案

初中毕业升学考试指导系列答案

学生课程精巧训练系列答案

名师点睛学练考系列答案

南大励学小学生英语四合一阅读组合训练系列答案

学业测评课时练测加全程测控系列答案

学业水平考试全景训练系列答案

正宗十三县系列答案

相关题目

6．求圆心在A（4，$\frac{5π}{6}$）处且过极点的圆的极坐标方程，并把它化为圆的标准方程．

7．已知α终边在第四象限，确定下列各角终边所在的象限：
（1）$\frac{α}{2}$；（2）2α；（3）$\frac{α}{3}$；（4）3α．

4．在△ABC中，内角A，B，C的对边分别为a，b，c．已知2sin2A+sin（2B+C）=sinC，且c=2，C=$\frac{π}{3}$．则△ABC的面积为$\frac{2\sqrt{3}}{3}$．

11．函数y=sinx在[$\frac{3}{2}π$，α]上单调递增，则α的取值范围是（$\frac{3}{2}π$，$\frac{5π}{2}$]．

1．在等差数列{a_n}中，若a₆+a₁₅=10，则前20项的和S₂₀=（　　）

8．求证：$\frac{2sin（0-\frac{3π}{2}）cos（0+\frac{π}{2}）-1}{1-2si{n}^{2}0}$=$\frac{tan（9π+0）+1}{tan（π+0）-1}$．

2．函数f（x）的导函数f′（x）的图象如图所示，则（　　）

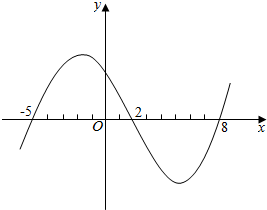
	A．	f（-2）＞f（1）		B．	f（-2）＜f（1）
	C．	f（-2）=f（1）		D．	f（-2）与f（1）的大小不能确定

3．记a=1.8²⁰¹⁶+0.2²⁰¹⁶，b=2²⁰¹⁶，则它们的大小关系为（　　）

以上均有可能