题目内容
将圆![]() 上的点的横坐标保持不变,纵坐标变为原来的
上的点的横坐标保持不变,纵坐标变为原来的![]() 倍,得到曲线
倍,得到曲线![]() .设直线
.设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,其中
,其中![]() 是曲线
是曲线![]() 与
与![]() 轴正半轴的交点.
轴正半轴的交点.
(Ⅰ)求曲线![]() 的方程;
的方程;
 (Ⅱ)证明:直线
(Ⅱ)证明:直线![]() 的纵截距为定值.
的纵截距为定值.
![]() ;
;![]()
解析:
(Ⅰ)设所求曲线![]() 上的任一点坐标为
上的任一点坐标为![]() ,圆
,圆![]() 上的对应点的坐标为
上的对应点的坐标为![]() ,由题意可得
,由题意可得 ,
,
![]()
![]() ,
,![]() ,即
,即
![]() 曲线
曲线![]() 的方程为
的方程为![]() .
.
![]() (Ⅱ)
(Ⅱ)![]() ,显然直线
,显然直线![]() 与
与![]() 轴不垂直,设直线
轴不垂直,设直线![]() ,与椭圆
,与椭圆![]() :
:![]() 相交于
相交于![]() ,
,
由 得
得![]() ,
,
![]() ,
, ![]()
![]() ,
,![]() ,
,
即:![]()
![]() ,
,
![]() ,
,
整理得:![]() ,
,
即![]() ,
,
![]() ,
,![]() ,
,
展开得:![]() ,
,![]() ,
,
![]() 直线
直线![]() 的纵截距为定值
的纵截距为定值![]() .
.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 上各点的纵坐标压缩至原来的
上各点的纵坐标压缩至原来的 ,所得曲线记作C;将直线3x-2y-8=0
,所得曲线记作C;将直线3x-2y-8=0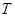 是将平面上每个点
是将平面上每个点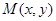 的横坐标乘2,纵坐标乘4,变到点
的横坐标乘2,纵坐标乘4,变到点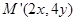 。
。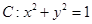 在变换
在变换 上各点的纵坐标不变,横坐标缩短为原来的
上各点的纵坐标不变,横坐标缩短为原来的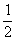 ,得到一个椭圆,则该椭圆的离心率为
,得到一个椭圆,则该椭圆的离心率为
 C.
C. D.
D.