Question

将圆x²+y²=4上各点的纵坐标变为原来的一半（横坐标保持不变），得到曲线C．

⑴ 求曲线C的方程；

⑵ 设O为坐标原点，过点F(, 0)的直线l交曲线C于A、B两点，N为线段AB的中点，延长线段ON交曲线C于点E，求证：的充要条件是AB=3．

Answer 1

解．⑴设P(x₀, y₀)为圆C上任意一点，Q(x, y)的横坐标与P相同，纵坐标为P的一半，

即x₀= x,  y₀=2y    

又P(x₀, y₀)满足x₀²+y₀² = 4   则x²+4y² = 4

即 求曲线C的方程为     

⑵当l的斜率不存在时，、 AB=3都不成立； 

当l的斜率存在时，设斜率为k，

则A、B两点的坐标(x₁, y₁)、(x₂,y₂)是方程组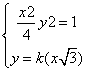的解

整理，得：(1＋4k²)x²8k²x＋12k²4 =0

x₁＋x₂=, x₁x₂=      

∴N的坐标为x_N = ，y_N= k(x_N－) =

∴ON的方程为y= x

与C的方程联立，得  

必要性（→AB=3）：由得 =2× =2 x_N

       ∴ k²=      

此时 AB=…=a－ex₁＋a－ex₂=2a－e(x₁＋x₂)=4－×=3

       ∴充分性成立

充分性（AB=3→）：

AB=…=a－ex₁＋a－ex₂=2a－e(x₁＋x₂)=4－×=3

       ∴ k²=

∴ = ，x_N = =  

∴ x_E =2 x_N            又E、N共线

       ∴必要性成立

综上，的充要条件是AB=3．