题目内容
20.已知sinα+cosα=$\frac{1}{3}$,其中0<α<π,求sinα-cosαθ的值.分析 将sinα+cosα=$\frac{1}{3}$两边平方,利用平方关系化简求出2sinαcosα的值,根据三角函数的符号缩小α的范围,判断出sinα-cosα的符号,利用平方关系求出sinα-cosα的值.
解答 解:将sinα+cosα=$\frac{1}{3}$两边平方得,
2sinαcosα=$-\frac{8}{9}$<0,
因为0<α<π,所以$\frac{π}{2}$<α<π,
则sinα-cosα>0,
所以sinα-cosα=$\sqrt{(sinα-cosα)^{2}}$=$\sqrt{1-(-\frac{8}{9})}$=$\frac{\sqrt{17}}{3}$.
点评 本题考查同角三角函数的平方关系,以及三角函数的符号,属于中档题.

练习册系列答案
相关题目
8.已知长方体的底面是正方形,且边长为2,体对角线长为2$\sqrt{5}$,则它的表面积为( )
| A. | 4(3$\sqrt{3}$+4) | B. | 8(2$\sqrt{3}$+1) | C. | 12(2$\sqrt{3}$+1) | D. | 3($\sqrt{3}$+8) |
5.如果一条直线与一个平面平行,则这条直线与这个平面内直线的位置关系为( )
| A. | 平行或相交 | B. | 平行或异面 | C. | 相交或异面 | D. | 都有可能 |
9.已知抛物线y2=12x上两点P(x1,y1)、Q(x2,y2),且x1+x2=8,则|PQ|的最大值为( )
| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
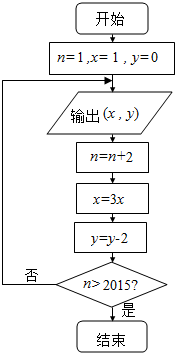 某算法的流程图如图所示,记输出的数组(x,y)依次为(x1,y1),(x2,y2),…(x3,y3)…,若程序运行中输出的一个数组是(9,y),则y=-4;程序结束时,共输出(x,y)的组数为1008.
某算法的流程图如图所示,记输出的数组(x,y)依次为(x1,y1),(x2,y2),…(x3,y3)…,若程序运行中输出的一个数组是(9,y),则y=-4;程序结束时,共输出(x,y)的组数为1008.