题目内容
已知各项全不为零的数列{an}的前n项和为Sn,且Sn=
anan+1(n∈N*),其中a1=1.则an=
| 1 |
| 3 |
an=
;
|
|
an=
;
.
|
|
分析:由题意可得Sn-1=
an-1an,与已知式子相减可得an+1-an-1=3,即数列的奇数项,和偶数项均为公差为3的等差数列,由等差数列的通项公式分别可得.
| 1 |
| 3 |
解答:解:由题意可得
,
①-②可得:an=
an(an+1-an-1),
∵an≠0,∴an+1-an-1=3,
又∵a1=1,a2=3;
∴an=
,
,
故答案为:an=
,
|
|
①-②可得:an=
| 1 |
| 3 |
∵an≠0,∴an+1-an-1=3,
又∵a1=1,a2=3;
∴an=
|
|
故答案为:an=
|
|
点评:本题考查数列通项公式的求解,分类求解是解决问题的关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
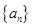 的前
的前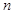 项和为
项和为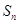 ,且
,且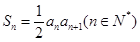 ,其中
,其中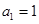
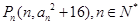 ,试求直线
,试求直线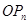 斜率的最小值(
斜率的最小值(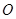 为坐标原点).
为坐标原点). N*),其中a1=1.
N*),其中a1=1. (k=1,2,…,n-1),b1=1.
(k=1,2,…,n-1),b1=1.