题目内容
(本小题满分10分)选修4—1:几何证明选讲
如图,已知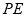 切⊙
切⊙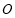 于点
于点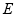 ,割线
,割线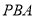 交⊙
交⊙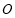 于
于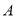 、
、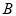 两点,
两点, 的平分线和
的平分线和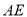 、
、 分别交于点
分别交于点 、
、 .求证:
.求证:
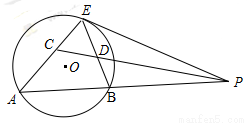
(1)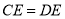 ;
;
(2)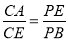 .
.
(1)证明见解析;(2)证明见解析
【解析】
试题分析:(1)从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线,平分两条切线的夹角;(2)判断三角形相似:一是平行于三角形一边的直线截其它两边所在的直线,截得的三角形与原三角形相似;二是如果一个三角形的两个角与另一个三角形的两个角对应相等, 那么这两个三角形相似;三是如果两个三角形的两组对应边的比相等,并且相应的夹角相等, 那么这两个三角形相似;四是如果两个三角形的三组对应边的比相等,那么这两个三角形相似;五是对应角相等,对应边成比例的两个三角形叫做相似三角;(3)切割线定理:切割线定理,是圆幂定理的一种,从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.
试题解析:(1)  切⊙
切⊙ 于点
于点 ,
,

 平分
平分

 ,
,
 5分
5分
(2) 
 ∽
∽

同理 ∽
∽ ,
,


 10分
10分
考点:1、切割线定理的应用;2、三角形相似的应用.
考点分析: 考点1:几何证明选讲 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的正视图是边长为4的正方形,则此正三棱柱的侧视图的面积为( )
的正视图是边长为4的正方形,则此正三棱柱的侧视图的面积为( )

 D.
D.


 ,
, ,且
,且 ,则
,则 ,
, .
. ,则它的渐近线方程为( )
,则它的渐近线方程为( ) B.
B. C.
C. D.
D.
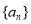 中,已知
中,已知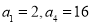 .
.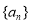 的通项公式.
的通项公式.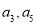 分别为等差数列
分别为等差数列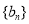 的第3项和第5项,试求数列
的第3项和第5项,试求数列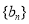 的前
的前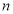 项和
项和 .
. 中,设
中,设 是曲线
是曲线 :
: 上任意一点,
上任意一点, 是曲线
是曲线 交坐标轴于
交坐标轴于 ,
, 两点,则以下结论正确的是
两点,则以下结论正确的是 的面积为定值
的面积为定值



 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,已知
,已知 .
. 的大小;
的大小;  ,求
,求 的取值范围.
的取值范围.
 时,解不等式
时,解不等式 ;
; ,使得,
,使得, 成立,求实数
成立,求实数 的取值范围.
的取值范围.