题目内容
已知a∈R,函数f(x)=x|x-a|
(Ⅰ)当a=4时,写出函数f(x)的单调递增区间;
(Ⅱ)当a=4时,求f(x)在区间(1,
)上的最值;
(Ⅲ)设a≠0函数f(x)在(p,q)上既有最大值又有最小值,请分别求出p,q的取值范围(用a表示).
(Ⅰ)当a=4时,写出函数f(x)的单调递增区间;
(Ⅱ)当a=4时,求f(x)在区间(1,
| 9 |
| 2 |
(Ⅲ)设a≠0函数f(x)在(p,q)上既有最大值又有最小值,请分别求出p,q的取值范围(用a表示).
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)当a=4时,f(x)=
,由此利用导数性质能求出单调增区间.
(Ⅱ)由f′(x)=
,f′(x)<0,得2<x<4,由此利用导数性质能求出f(x)在区间(1,
)上的最值.
(3)f(x)=
,作出函数的图象,利用数形结合思想能求出p,q的取值范围.
|
(Ⅱ)由f′(x)=
|
| 9 |
| 2 |
(3)f(x)=
|
解答:
解:(Ⅰ)当a=4时,f(x)=x|x-4|,
∴f(x)=
,
∴f′(x)=
,由f′(x)>0,得x>4或x<2,
∴单调增区间为(-∞,2],[4,+∞).…(4分)
(Ⅱ)∵f(x)=
,
∴f′(x)=
,
由f′(x)<0,得2<x<4,
f(x)在区间(1,
)上的最值为:
f(x)max=f(2)=4,f(x)min=f(4)=0…(8分)
(3)f(x)=
,…(10分)
①当a>0时,图象如图1所示.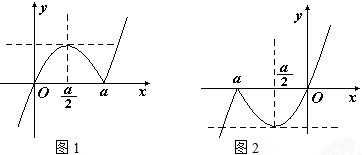
由
得x=
.
∴0≤p<
,a<q≤
a.…(12分)
②当a<0时,图象如图2所示.
由
得x=
a.
∴
a≤p<a,
<q≤0.…(14分)
∴f(x)=
|
∴f′(x)=
|
∴单调增区间为(-∞,2],[4,+∞).…(4分)
(Ⅱ)∵f(x)=
|
∴f′(x)=
|
由f′(x)<0,得2<x<4,
f(x)在区间(1,
| 9 |
| 2 |
f(x)max=f(2)=4,f(x)min=f(4)=0…(8分)
(3)f(x)=
|
①当a>0时,图象如图1所示.
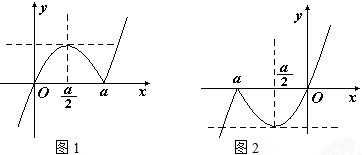
由
|
(
| ||
| 2 |
∴0≤p<
| a |
| 2 |
| ||
| 2 |
②当a<0时,图象如图2所示.
由
|
1+
| ||
| 2 |
∴
| ||
| 2 |
| a |
| 2 |
点评:本题考查的单调区间的求法,考查函数最值的求法,考查实数取值范围的求法,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 设函数f(x)=
设函数f(x)=