题目内容
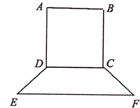 要制作一个如图的框架(单位:米),要求所围成的总面积为19.5(米2),其中ABCD是一个矩形,EFCD是一个等腰梯形,梯形高h=
要制作一个如图的框架(单位:米),要求所围成的总面积为19.5(米2),其中ABCD是一个矩形,EFCD是一个等腰梯形,梯形高h= AB,tan∠FED=
AB,tan∠FED= ,设AB=x米,BC=y米.
,设AB=x米,BC=y米.
(Ⅰ)求y关于x的表达式;
(Ⅱ)如何设计x,y的长度,才能使所用材料最少?
解:(1)如图,等腰梯形EFCD中,DH是高,

依题意:DH= AB=
AB= x,EH=
x,EH= =
= =
=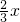 ,
,
∴ =xy+
=xy+ (x+x+
(x+x+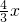 )
) =xy+
=xy+ ,∴y=
,∴y= ,
,
∵x>0,y>0,∴ ,解得0<x<
,解得0<x< ,
,
∴所求的表达式为:y= ,(0<x<
,(0<x< )
)
(2)在RT△DEH中,∵tan∠FED= ,∴sin∠FED=
,∴sin∠FED= ,
,
∴DE= =
= =
= ,
,
∴l=(2x+2y)+2× +(2×
+(2× )=2y+6x
)=2y+6x
= =
= +
+ ≥2
≥2 =26,
=26,
当且仅当 =
= ,即x=3时取等号,此时y=
,即x=3时取等号,此时y= =4,
=4,
∴AB=3米,BC=4米时,用材料最少
分析:(1)依题意可表示出梯形的高,和底边长,进而可得表示面积,可建立x,y的关系式,化为函数式即可;(2)RT△DEH中,可表示出DE,进而可得l=2y+6x= +
+ ,由基本不等式可得答案.
,由基本不等式可得答案.
点评:本题考查求函数解析的方法,涉及基本不等式的应用,属中档题.

依题意:DH=
 AB=
AB= x,EH=
x,EH= =
= =
=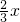 ,
,∴
 =xy+
=xy+ (x+x+
(x+x+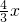 )
) =xy+
=xy+ ,∴y=
,∴y= ,
,∵x>0,y>0,∴
 ,解得0<x<
,解得0<x< ,
,∴所求的表达式为:y=
 ,(0<x<
,(0<x< )
)(2)在RT△DEH中,∵tan∠FED=
 ,∴sin∠FED=
,∴sin∠FED= ,
,∴DE=
 =
= =
= ,
,∴l=(2x+2y)+2×
 +(2×
+(2× )=2y+6x
)=2y+6x=
 =
= +
+ ≥2
≥2 =26,
=26,当且仅当
 =
= ,即x=3时取等号,此时y=
,即x=3时取等号,此时y= =4,
=4,∴AB=3米,BC=4米时,用材料最少
分析:(1)依题意可表示出梯形的高,和底边长,进而可得表示面积,可建立x,y的关系式,化为函数式即可;(2)RT△DEH中,可表示出DE,进而可得l=2y+6x=
 +
+ ,由基本不等式可得答案.
,由基本不等式可得答案.点评:本题考查求函数解析的方法,涉及基本不等式的应用,属中档题.

练习册系列答案
相关题目
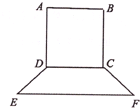 要制作一个如图的框架(单位:米),要求所围成的总面积为19.5(米2),其中ABCD是一个矩形,EFCD是一个等腰梯形,梯形高h=
要制作一个如图的框架(单位:米),要求所围成的总面积为19.5(米2),其中ABCD是一个矩形,EFCD是一个等腰梯形,梯形高h=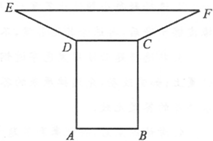 (2012•湛江二模)要制作一个如图的框架(单位:米),要求所围成的面积为6米2,其中ABCD是一个矩形,EFCD是一个等腰梯形,EF=3CD,tan∠FED=
(2012•湛江二模)要制作一个如图的框架(单位:米),要求所围成的面积为6米2,其中ABCD是一个矩形,EFCD是一个等腰梯形,EF=3CD,tan∠FED= AB,tan∠FED=
AB,tan∠FED= ,设AB=x米,BC=y米.
,设AB=x米,BC=y米.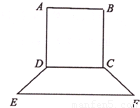
 ,设AB=x米,BC=y米.
,设AB=x米,BC=y米.