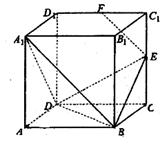
题目内容
如图,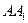 、
、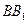 为圆柱
为圆柱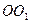 的母线,
的母线,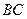 是底面圆
是底面圆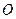 的直径,
的直径,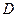 、
、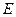 分别是
分别是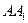 、
、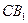 的中点,
的中点,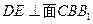 .
.
(1)证明: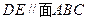 ;
;
(2)求四棱锥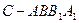 与圆柱
与圆柱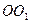 的体积比;
的体积比;
(3)若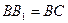 ,求
,求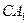 与面
与面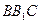 所成角的正弦值.
所成角的正弦值.
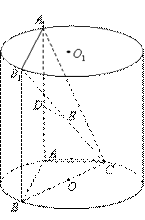
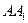 、
、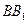 为圆柱
为圆柱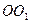 的母线,
的母线,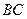 是底面圆
是底面圆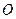 的直径,
的直径,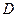 、
、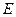 分别是
分别是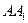 、
、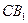 的中点,
的中点,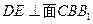 .
.(1)证明:
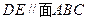 ;
;(2)求四棱锥
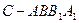 与圆柱
与圆柱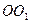 的体积比;
的体积比;(3)若
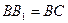 ,求
,求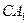 与面
与面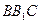 所成角的正弦值.
所成角的正弦值.
解:(1)证明:连结 ,
, .
. 分别为
分别为 的中点,∴
的中点,∴ .
.
又 ,且
,且 .∴四边形
.∴四边形 是平行四边形,
是平行四边形,
即 . ∴
. ∴ . ………………………4分
. ………………………4分
(2)由题 ,且由(1)知
,且由(1)知 .∴
.∴ ,∴
,∴  ,∴
,∴ .
.
因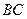 是底面圆
是底面圆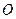 的直径,得
的直径,得 ,且
,且 ,
,
∴ ,即
,即 为四棱锥的高.设圆柱高为
为四棱锥的高.设圆柱高为 ,底半径为
,底半径为 ,
,
则 ,
,
∴ :
:
 . ………………………9分
. ………………………9分
(3)解一:由(1)(2)可知,可分别以 为坐标轴建立空间直角标系,如图
为坐标轴建立空间直角标系,如图
设 ,则
,则 ,
, ,
, ,从而
,从而 ,
,
 ,由题,
,由题, 是面
是面 的法向量,设所求的角为
的法向量,设所求的角为 .
.
则 . …………………14分
. …………………14分
解二:作过 的母线
的母线 ,连结
,连结 ,则
,则 是上底面圆
是上底面圆 的直径,连结
的直径,连结 ,
,
得
 ,又
,又 ,∴
,∴ ,连结
,连结 ,
,
则 为
为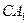 与面
与面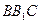 所成的角,设
所成的角,设 ,则
,则
 ,
, .……12分
.……12分
在 中,
中,

 ,
, .
. 分别为
分别为 的中点,∴
的中点,∴ .
. 又
 ,且
,且 .∴四边形
.∴四边形 是平行四边形,
是平行四边形,即
 . ∴
. ∴ . ………………………4分
. ………………………4分(2)由题
 ,且由(1)知
,且由(1)知 .∴
.∴ ,∴
,∴  ,∴
,∴ .
. 因
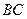 是底面圆
是底面圆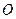 的直径,得
的直径,得 ,且
,且 ,
,∴
 ,即
,即 为四棱锥的高.设圆柱高为
为四棱锥的高.设圆柱高为 ,底半径为
,底半径为 ,
,则
 ,
,
∴
 :
:
 . ………………………9分
. ………………………9分(3)解一:由(1)(2)可知,可分别以
 为坐标轴建立空间直角标系,如图
为坐标轴建立空间直角标系,如图设
 ,则
,则 ,
, ,
, ,从而
,从而 ,
, ,由题,
,由题, 是面
是面 的法向量,设所求的角为
的法向量,设所求的角为 .
. 则
 . …………………14分
. …………………14分解二:作过
 的母线
的母线 ,连结
,连结 ,则
,则 是上底面圆
是上底面圆 的直径,连结
的直径,连结 ,
,得

 ,又
,又 ,∴
,∴ ,连结
,连结 ,
,则
 为
为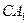 与面
与面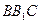 所成的角,设
所成的角,设 ,则
,则 ,
, .……12分
.……12分在
 中,
中,

略

练习册系列答案
相关题目
 中
中 ,
, 是
是 的中点,
的中点, ,垂足为
,垂足为 .求证:
.求证: .
.
 ,M、N分别为DE与DB的中点,且MN=1.
,M、N分别为DE与DB的中点,且MN=1.
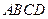 中,
中,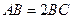 ,
,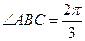 ,
,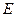 为线段
为线段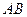 的中线,将△
的中线,将△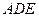 沿
沿 直线
直线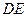 翻折成△
翻折成△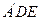 ,使平面
,使平面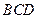 ,
,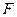 为线
为线 段
段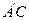 的中点.
的中点.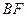 ∥平面
∥平面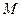 为线段
为线段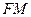 与平面
与平面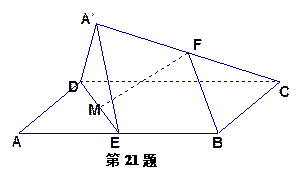
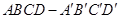 中,
中,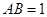 ,
,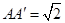 ,则
,则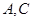 两点间的球面距离为
两点间的球面距离为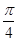
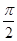
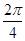
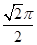
 的底面是正方形,侧棱
的底面是正方形,侧棱 平面
平面  ,且
,且 ,则异面直线
,则异面直线 所成角的余弦值为( )
所成角的余弦值为( )




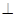 面BDE,并说明理由。
面BDE,并说明理由。